What is grashof number?
Grashof number is defined as the ratio of the product of inertia force and buoyant force to the square of viscous force present in the fluid.
Grashof number is denoted by the symbol of ‘Gr‘.
As per the definition of the Grashof number,
Grashoff number (Gr) =
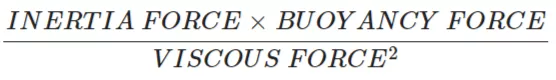
Where,
Inertia force = `\rho .V^{2}.L^{2}`
Buoyancy force = ρ.g.`L^{3}`.β.∆T
Viscous force = μLV
By putting these values in the above equation we get,
Gr = `\frac{\rho V^{2}L^{2}\times \rho gL^{3}\beta \Delta T}{(\mu LV)^{2}}`
Gr = `\frac{\rho ^{2} gL^{3}\beta \Delta T}{\mu^{2}}` or `\frac{gL^{3}\beta \Delta T}{\nu^{2}}`
This is the required equation for grashoff number.
Where,
ρ = Density of fluid
β = Coefficient of expansion
∆T = Temperature difference
μ = Dynamic viscosity
`\nu` = Kinematic viscosity
Significance of grashof number in heat transfer:
The physical significance of grashof number are as follows:-
1) The grashoff number provides the relation between inertia force, buoyant force, and viscous force in flow of fluid.
2) This dimensionless number is used in the analysis of free convection heat transfer.
3) The grashoff number has the same importance in free convection as the Reynolds number has in forced convection.
4) Grashoff number helps to find the type of flow (laminar, transition, turbulent) in free convection.
Grashoff number examples:
Here are some solved numericals to understand, how to calculate grashof number.
1) Check the flow is laminar or turbulent the properties of the fluid are given below,
Characteristics length of body, L = 6 m
Surface temperature (`T_{s}`) = 650 K
Fluid temperature (`T_{∞}`) = 450 K
Kinematic viscosity (`\nu `) = 0.2 × `10^(-3)` m²/s
Solution:-
The coefficient of volumetric expansion is given by,
β = `\frac{2}{T_{S}+T_{\infty}}`=`\frac{2}{650+450}`
β = 1.81 x `10^{-3}`
The grashoff number is given by,
Gr = `\frac{gL^{3}\beta (T_{S}-T_{\infty }) }{\nu^{2}}`
Gr = `\frac{9.81\times 6^{3}\times (1.81\times 10^{-3}) (650-450) }{(0.2\times 10^{-3})^{2}}`
Gr = 1.917 x `10^{10}`
Here, Gr > `10^{9}`, Therefore the given flow is in a turbulent state.
2) The sphere at 600 K with a characteristic length of 5.5 m is cooled by the gas at 300 K by free convection. If the cooling gas is considered as ideal and if the kinematic viscosity is 0.25 × `10^{-3}` `m^{2}`/s, find the type of flow over the surface.
Solution:-
Given:
L = 5.5 m
`T_{s}` = 600 K
`T_{∞}`= 300 K
`\nu` = 0.25 × `10^{-3}` m²/s
β = `\frac{2}{T_{S}+T_{\infty}}`=`\frac{2}{600+300}`
β = 2.22 x `10^{-3}`
For free convection, the grashoff number is given by,
Gr = `\frac{gL^{3}\beta (T_{S}-T_{\infty }) }{\nu^{2}}`
Now the grashoff number is given by,
Gr = `\frac{9.81\times 5.5^{3}\times (2.22\times 10^{-3}) (600-300) }{(0.25\times 10^{-3})^{2}}`
Gr = 1.73 × `10^{10}`
As Gr > `10^{9}`, Therefore the given flow is in a turbulent state.
Read also: