The critical radius of insulation & the critical thickness of insulation are the necessary factors in the case of insulation over the cylindrical or spherical surface.
For the insulation applied over a spherical or cylindrical surface, up to a certain radius the insulation the rate of heat transfer from the object increases.
The radius of insulation where the heat transfer from the object is maximum is known as the critical radius of insulation & The thickness of insulation at a critical radius is known as the critical thickness of insulation.
In this article, we’re going to discuss:
- What is Critical radius of insulation?
- Critical thickness of insulation:
- Critical radius of insulation graph:
- Significance of Critical radius & thickness of insulation:
- Critical radius and thickness of insulation for cylinder:
- Critical radius and thickness of insulation for sphere:
- Why rate of heat transfer increase till the critical radius of insulation?
- Solved Numerical:
- FAQ:
What is Critical radius of insulation?
The critical radius of insulation is the outer radius of insulation at which the rate of heat transfer through the body is maximum. Or it is the radius of insulation at which the insulation has a minimum thermal resistance.
As shown in the below figure, the rate of heat transfer increases with an increase in the thickness of insulation up to the critical radius of insulation and then it starts decreasing.
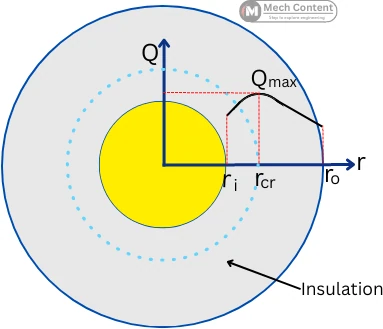
The insulation is used to reduce the heat loss from the object. But in the case of insulation to the cylinder or sphere, there is a certain insulation thickness that is not helpful in decreasing the rate of heat transfer from the surface of the object.
It means that up to the critical radius, instead of decreasing the heat transfer, the insulation increases the heat transfer rate.
If we increase the thickness more than the critical thickness value, then the heat transfer rate starts to decrease.
The critical radius of insulation depends on the thermal conductivity (K) of insulation and convective heat transfer coefficient (h) at the surround of the insulation.
For the cylinder, the critical radius of insulation (rcr) is given by,
`\mathbf{r_{cr} = \frac{K}{h}}`
For the sphere, the critical radius of insulation is given by,
`\mathbf{r_{cr} = \frac{2K}{h}}`
Critical thickness of insulation:
The thickness of insulation at which the heat transfer reaches the maximum value is the critical thickness of insulation.
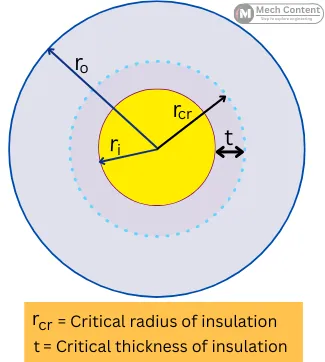
It is the thickness of the insulation up to the critical radius. It is given by, the difference between the critical radius and the inner radius of insulation.
Critical thickness = Critical radius of insulation – Inner radius of insulation
`t=r_{cr}-r_{i}`
Critical radius of insulation graph:
This graph indicates the variation in heat transfer rate with the increase in the thickness of insulation.
In the below graph at a certain radius of insulation (rcr), the rate of heat transfer stops increasing (Qmax), this radius indicates the critical radius of insulation. While the thickness of the insulation is called the critical thickness of insulation.
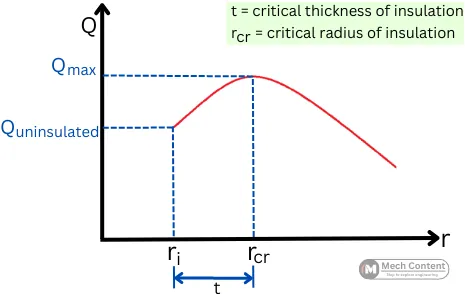
The variation of outer radius of insulation (ro) with respect to the critical radius rcr, affects the heat transfer rate as follows:
A] For ro < rcr [outer radius is below critical radius]:
The insulation on a surface up to the radius rcr causes a rise in the rate of heat transfer through the insulating body.
The rise in insulation up to the critical radius causes thermal resistance to decrease. Thus, it results in a rise in heat transfer rate.
B] For ro = rcr [outer radius is equal to critical radius]:
At the critical radius of insulation, the thermal resistance is minimum hence the heat transfer rate is maximum (Qmax).
Up to the critical radius, the outside area exposed to the surroundings increases. Here the increase in conduction resistance is dominated by an increase in convective heat transfer.
C] For ro > rcr [outer radius more than critical radius]:
If the radius of insulation increases further of the rcr, the conduction resistance starts to increase, therefore, the rate of heat transfer also goes on decreasing.
In this case, the increase in the rate of convective heat transfer is dominated by an increase in conductive resistance.
Significance of Critical radius & thickness of insulation:
The critical thickness of insulation and critical radius of insulation has the following significance based on their purpose:
1) For thermal insulation:
Thermal insulation is used to avoid or lower the rate of heat transfer from objects. Hence, in this case, the thickness of insulation should be greater than the critical thickness of insulation.
2) For electric insulators:
The insulations used for the electric conductors are good insulators for electricity and good conductors for heat.
Therefore, in this case the radius of insulation should be equal to or less than the critical radius of insulation. So that it will resist the flow of electricity but allow the transfer of heat that is generated while electricity conduction.
Critical radius and thickness of insulation for cylinder:
The formula for the critical radius of insulation for the cylindrical surface is given by,
`r_{cr}=\frac{K}{h}`
Here,
K= Thermal conductivity, w/mK
h= Convective heat transfer coefficient, w/m2.K
The critical thickness of insulation for the cylinder is given by,
`\text{Critical thickness, }t_{\text{cylinder}}=r_{cr}-r_{i}`
`t_{\text{cylinder}}=\frac{K}{h}-r_{i}`
Where, ri = inner radius of insulation.
Derivation for Critical radius of insulation for cylinder:
The below figure shows the insulated cylindrical object with insulation having an inner radius ri and outer radius ro.
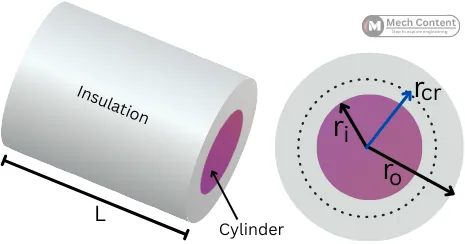
The total thermal resistance by the insulation is given by,
Rth = Rcond. + Rconv.
As for cylinders, `R_{cond.} = \frac{ln(\frac{r_{o}}{r_{i}})}{2\piKL}` and `R_{conv.} = \frac{1}{h.(2\pir_{o}.L)}`,
`\therefore\ R_{th} = \frac{ln(\frac{r_{o}}{r_{i}})}{2\piKL} +\frac{1}{h.(2\pir_{o}.L)}`
At the critical radius of insulation (ro = rcr), the thermal resistance of the insulation is minimum.
Therefore at ro = rcr,
`\frac{dR_{th}}{dr_{o}} = 0`
`\frac{d}{dr_{o}}[\frac{ln(\frac{r_{o}}{r_{i}})}{2\piKL} +\frac{1}{h.(2\pir_{o}.L)}] = 0`
`\frac{1}{2\pi.L}.\frac{d}{dr_{o}}[\frac{ln(\frac{r_{o}}{r_{i}})}{K}+\frac{1}{h.r_{o}}] = 0`
`\frac{d}{dr_{o}}[\frac{ln(\frac{r_{o}}{r_{i}})}{K}+\frac{1}{h.r_{o}}] = 0`
`\frac{d}{dr_{o}}[\frac{ln(\frac{r_{o}}{r_{i}})}{K}] + \frac{d}{dr_{o}}[\frac{1}{h.r_{o}}] = 0`
`[\frac{1}{K}.\frac{1}{\frac{r_{o}}{r_{i}}}.\frac{1}{r_{i}}] + [\frac{1}{h}.\frac{-1}{r_{o}^{2}}] = 0`
`\frac{1}{K.r_{o}} – \frac{1}{r_{o}^{2}.h} = 0`
`\frac{1}{K.r_{o}} = \frac{1}{r_{o}^{2}.h}`
`r_{o} = \frac{K}{h}`
`\therefore\ r_{cr} = r_{o} = \frac{K}{h}`
Critical radius and thickness of insulation for sphere:
The formula for the critical radius of insulation for the spherical surface is given by,
`r_{cr}=\frac{2K}{h}`
The critical thickness of insulation for the sphere is given by,
`\text{Critical thickness, }t_{\text{sphere}}=r_{cr}-r_{i}`
`t_{\text{sphere}}=\frac{2K}{h}-r_{i}`
Derivation for Critical radius of insulation for sphere:
The below figure shows the insulated sphere with the insulation having an inner radius of ri and an outer radius of ro.
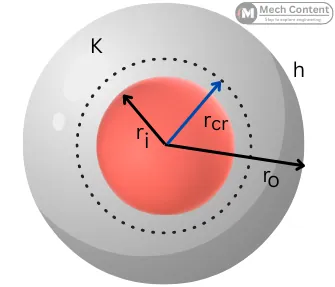
The conduction resistance of the spherical insulation is given by,
`R_{cond.} = \frac{r_{o}-r_{i}}{4\pi.Kr_{i}r_{o}}`
The convective resistance outside of the sphere is given by,
`R_{conv.} = \frac{1}{h.A} = \frac{1}{h.(4\pir_{o}^{2})}`
The total thermal resistance of insulation is given by,
Rth = Rcond. + Rconv.
`R_{th} = \frac{r_{o}-r_{i}}{4\pi.Kr_{i}r_{o}} + \frac{1}{h.(4\pir_{o}^{2})}`
At the critical radius of insulation, Rth is minimum.
`\therefore \frac{dR_{th}}{dr_{o}} = 0`
`\frac{d}{dr_{o}}[\frac{r_{o}-r_{i}}{4\pi.Kr_{i}r_{o}} + \frac{1}{h.(4\pir_{o}^{2})}] = 0`
`\frac{1}{4\pi}.\frac{d}{dr_{o}}[\frac{r_{o}}{Kr_{i}r_{o}}-\frac{r_{i}}{Kr_{i}r_{o}}+\frac{1}{h.r_{o}^{2}}] = 0`
`\frac{d}{dr_{o}}[\frac{1}{Kr_{i}}-\frac{1}{Kr_{o}}+\frac{1}{h.r_{o}^{2}}] = 0`
`\frac{1}{K}.\frac{-1}{r_{o}^{2}} + \frac{1}{h}.\frac{-2}{r_{0}^{3}} = 0`
`\frac{1}{Kr_{o}^{2}} = \frac{2}{hr_{o}^{3}}`
`r_{o} = \frac{2K}{h}`
`\therefore\ r_{cr} = r_{o} = \frac{2K}{h}`
Why rate of heat transfer increase till the critical radius of insulation?
As we increase the layer of insulation on a cylindrical or spherical surface, the area exposed to the surrounding also increases.
The convective heat transfer from outer surface is given by,
`Q_{conv.} = \frac{\Deltat}{h.A}`
As per the above equation, the increased surface area (A), increases the convective heat transfer.
Up to the critical radius, the conductive resistance of the added insulation is dominated by rising convective heat transfer. Therefore, up to the critical radius of insulation, the rate of heat transfer increases.
Let’s explain with an example.
Consider cylindrical insulation with inner radius ri and outer radius ro.
The total thermal resistance is the sum of the conduction resistance of insulation and convective resistance at the outer surface,
Rth = Rcond. + Rconv.
For the cylinder, the conduction resistance and convection resistance are as follows,
`R_{cond.} = \frac{ln(\frac{r_{o}}{r_{i}})}{2\piKL}\cdots[1]`
`R_{conv.} = \frac{1}{h.A} = \frac{1}{h.(2\pir_{o}L)}\cdots[2]`
As per equation [1], as the outer radius (ro) increases, the conduction resistance of the insulation increases.
While as per equation [2], as the outer radius (ro) increases, the convection resistance decreases.
The addition of insulation over cylindrical or spherical surfaces increases the outer surface area subjected to the atmosphere. This causes the convective heat transfer to increase.
The overall effect of these resistances (Rcond. & Rconv.) causes the value of the overall thermal resistance (Rth) to decrease up to a certain radius and then it starts to increase.
Therefore, the heat transfer rate increases up to a certain radius of insulation and then it starts to decrease.
Solved Numerical:
Consider a steam flowing pipe is insulated with the material having a thermal conductivity of 0.055 W/mK. If the convective heat transfer coefficient is 2.5 w/m2K, find the critical radius of the insulation of the pipe. If the pipe diameter is 25 mm, find the critical thickness of the insulation.
Given:
K = 0.055 W/m.K
h = 2.5 w/m2.K
d1 = 25 mm, r1 = 12.5 mm
Solution:
For cylindrical pipe, the critical radius rcr is given by,
`r_{cr} = \frac{0.055}{2.5}`
rcr = 0.022 m = 22 mm
The critical thickness of insulation (t) for the steam pipe is given by,
t = rcr – r1 = 22 – 12.5 = 9.5 mm
FAQ:
-
What are the practical applications of the critical insulation radius?
1] Electric insulators: The outer radius of insulation in the electric insulators is taken less than or equal to the critical radius.
2] Thermal insulation: Insulation to pipes flowing steam or hot fluid requires an outer insulation radius of more than a critical radius. -
Why does heat transfer rise at first till the critical radius?
The increase in the outer radius of insulation increases the outer area exposed to the atmosphere. It boosts convection heat transfer. Hence heat transfer rises till the critical radius.
-
What is the sphere’s critical insulation radius?
For the sphere, the critical radius is equal to (2K/h).
Read also:
