The kinetic energy indicates the energy due to the motion of an object. Let’s see how this kinetic energy gets affected by the mass and velocity of a moving object.
Kinetic energy increases with an increase in the mass or velocity of the object. The kinetic energy is proportional to the object’s mass and the square of its velocity. Due to the square of velocity, the kinetic energy gets more affected by the velocity than the mass of an object.
So, Continue reading to know in detail how these factors affect K.E. with examples.
Contents:
How does Mass affect kinetic energy?
The Kinetic energy (K.E.) of the object of mass ‘m’ and velocity ‘V’ is given by,
`\text{Kinetic Energy (K.E.)} = \frac{1}{2}.mV^{2}`
As per the above equation, the kinetic energy of the object is directly proportional to the mass of the moving body.
`K.E. \propto m`
Thus for two different objects moving with the same velocity, the heavier object possesses higher kinetic energy than the lighter object.
It means that if the mass is doubled, the object’s Kinetic energy also gets doubled. Similarly if mass tripled then kinetic energy also gets tripled.
Here are some of the examples that explain how mass affects kinetic energy.
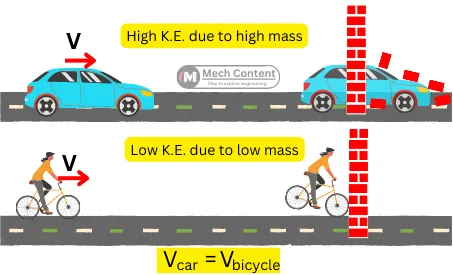
Consider a bicycle and a car moving with the same velocity to hit a wall. As the car has a high K.E. due to higher mass, the impact created by it can brake the wall.
While the bicycle possesses less K.E. due to less mass thus it will stop after hitting the wall.
Here’s another example:
The raindrops are lighter while hails (solid ice) has higher mass. Consider both falling with the same terminal velocity.
Due to less mass, raindrops possess less K.E., thus it hits with less impact while falling. While due to high mass, the hailstone possesses higher kinetic energy, thus it creates a high impact that can damage house roofs, cars, and living things too.

How does Velocity affect kinetic energy?
From the equation of kinetic energy, it is clear that the kinetic energy is directly proportional to the square of the velocity of the object.
`K.E. \propto V^{2}`
Thus, for the two objects having the same mass, the object having higher velocity possesses higher K.E. than the object moving with less velocity.
Or the kinetic energy of an object increases with an increase in its velocity.
Consider a van moving at the speed of 20 Kmph and then accelerating to 80 Kmph. Thus here by increasing speed, the K.E. of the van gets increased.

Here is another example:
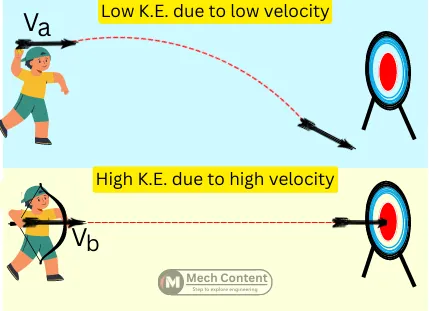
Assume the archer is throwing an arrow without using a bow. Due to the less velocity, this won’t be able to reach the target.
In another case, consider an archer used a bow to deliver an arrow. Now the bow helps the arrow to move with a much higher velocity.
Due to high velocity, the arrow possesses a high value of kinetic energy. Now because of higher K.E., the arrow can pierce into the target.
Why does Velocity have more effect on Kinetic energy than Mass?
The kinetic energy is proportional to the mass (m1) and square of the velocity (V2).
`K.E. = \frac{1}{2}.m.V^{2}`
Due to the square of velocity, a small change in velocity can cause a high change in Kinetic energy.
Thus, if you doubled the mass, the K.E. gets doubled, but if you doubled the velocity, the kinetic energy become 4 times of initial K.E.
Let me explain it with an example.
Consider the object of mass ‘m’ initially has kinetic energy `K.E_{i}`.
Now double the mass of the object, and the kinetic energy will become,
`KE_{f} = \frac{1}{2}.(2m).V^{2} = 2[\frac{1}{2}.(m).V^{2}]` `= 2. KE_{i}\cdots[1]`
Now in another case, double the velocity of the object. The kinetic energy will become,
`KE_{f} = \frac{1}{2}.m.(2V)^{2} = 4[\frac{1}{2}.(m).V^{2}]` `= 4. KE_{i}\cdots[2]`
Thus from [1] and [2], it is clear that the change in velocity affects kinetic energy more than the change in mass.
Related articles: