Hi friends, In the preceding article, we discussed the polar moment of inertia. In this post, we’ll go through the polar moment of inertia of a circle in detail.
In this article, we’re going to discuss:
- Polar moment of inertia of a circle:
- Polar moment of inertia circle formula:
- Polar moment of inertia of circle derivation:
3.1. For solid circle:-
3.2. For hollow circle:- - Polar moment of inertia of circle examples:
Polar moment of inertia of a circle:
The polar moment of inertia of circle is used for the analysis of objects with circular profiles subjected to the torsional or twisting load.
It helps to find the shear stresses across the cross-section of the circular shaft, axles, couplings, etc.
Polar moment of inertia circle formula:
The polar moment of the solid circle is given by,
| J = `\frac{\pi }{32} D^{4}` |
OR
| J = `\frac{\pi R^{4}}{2}` |
Where,
D = Diameter of circle
R = Radius of circle
The polar moment of inertia for hollow circular profile is given by,
| J = `\frac{\pi }{32}[D_{o}^{4}-D_{i}^{4}]` |
OR
| J = `\frac{\pi }{2}[R_{o}^{4}-R_{i}^{4}]` |
Where,
Do = Outer diameter
Di = Inner diameter
Ro = Outer radius
Ri = Inner radius
Polar moment of inertia of circle derivation:
A] For solid circle:-
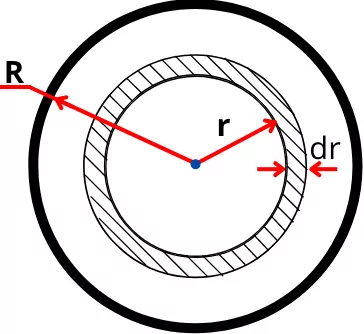
The above figure shows a circle of radius ‘R’. Consider a smaller portion of thickness ‘dr’ located at radius ‘r’ from the center.
The area of this smaller portion is given by,
dA = Perimeter x dr
dA = 2πr.dr
As per the definition of polar moment of inertia, the polar moment of inertia of a smaller portion is given by,
`J_{dA}` = `r^{2}.dA`
The total polar moment of inertia of the circle can be found by integrating the above equation.
J = `\int_{0}^{R}r^{2}.dA`
By putting the value of dA, the equation becomes,
J = `\int_{0}^{R}r^{2}.2\pi r.dr`
J = `2\pi\int_{0}^{R}r^{3}.dr`
J = 2π`[\frac{r^{4}}{4}]_{0}^{R}`
J = `2\pi[\frac{ R^{4}}{4}-0]`
| J = `\frac{\pi R^{4}}{2}` |
To find the polar moment of inertia in the form of diameter, put R = D/2 in the above equation.
J = `\frac{\pi (\frac{D}{2})^{4}}{2}`
| J = `\frac{\pi D^{4}}{32}` |
B] For hollow circle:-
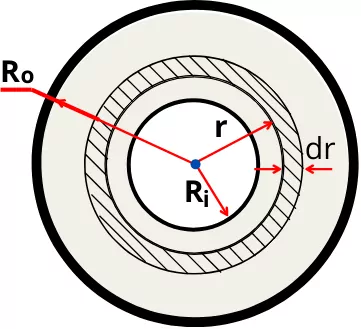
The above figure shows the hollow circle with an inner radius of `R_{i}` and an outer radius of `R_{o}`.
Consider a smaller portion of thickness ‘dr’, located at a distance ‘r’ from the center of the hollow circle.
The area of this small portion is given by,
dA = Perimeter x Thickness
dA = (2πr).dr
As per the definition, the polar moment of inertia of a smaller portion is given by,
`J_{dA}` = `r^{2}.dA`
The total polar moment of inertia of the circle can be found by integrating the above equation.
J = `\int_{Ri}^{Ro}r^{2}.dA`
By putting the value of dA, the equation becomes,
J = `\int_{Ri}^{Ro}r^{2}(2\pi r).dr`
J = `2\pi \int_{Ri}^{Ro}r^{3}.dr`
J = `2\pi [\frac{r^{4}}{4}]_{Ri}^{Ro}`
J = `2\pi [\frac{R_{o}^{4}}{4}-\frac{R_{i}^{4}}{4}]`
J = `\frac{2\pi[R_{o}^{4}-R_{i}^{4}]}{4}`
| J = `\frac{\pi }{2}[R_{o}^{4}-R_{i}^{4}]` |
To find the polar moment of inertia in the form of diameter, put Ro = Do/2 and Ri = Di/2 in the above equation.
J = `\frac{\pi }{2}[(\frac{D_{o}}{2})^{4}-(\frac{D_{i}}{2})^{4}]`
| J = `\frac{\pi }{32}[D_{o}^{4}-D_{i}^{4}]` |
Polar moment of inertia of circle examples:
1] A machine has a hollow circular shaft of an outer diameter of 80 mm and an inner diameter of 65 mm. Find the polar moment of inertia about the axis of the shaft.
Given:-
Do = 80 mm
Di = 65 mm
The polar moment of inertia for the hollow circular profile is given by,
J = `\frac{\pi }{32}[D_{o}^{4}-D_{i}^{4}]`
J = `\frac{\pi }{32}[80^{4}-65^{4}]`
| J = 2268757 mm⁴ |
This is the polar moment of inertia for the hollow circular shaft.
2] A solid shaft of length 1 m has a diameter of 40 mm and a hollow shaft of length 1.2 m has an outer diameter of 60 mm. If both the shafts are made by using the same amount of material then compare the polar moment of inertia of both shafts.
Given:-
Dsolid = 40 mm = 0.04 m
Lsolid = 1 m
DHollow(o) = 60 mm = 0.06 m
LHollow= 1.2 m
Step 1] Inner diameter of hollow shaft (`\mathbf{D_{\text{Hollow(i)}}}`):
As the both shafts are made up by using same amount of material.
∴ `V_{\text{solid}}` = `V_{\text{hollow}}`
∴ `A_{\text{solid}}` x `L_{S}` = `A_{\text{hollow}}` x `L_{H}`
`\frac{\pi }{4}D_{s}^{2}` x `L_{S}` = `\frac{\pi }{4}[D_{\text{H(o)}}^{2}-D_{\text{H(i)}}^{2}]` x `L_{H}`
`\frac{\pi }{4}\times 0.04^{2}` x 1 = `\frac{\pi }{4}[0.06^{2}-D_{\text{H(i)}}^{2}]` x 1.2
| `\mathbf{D_{\text{H(i)}}}` = 0.047 m |
Step 2] Polar moment of inertia of solid circle:
Polar moment of inertia of a solid circle is given by,
`J_{S}` = `\frac{\pi }{32}D_{S}^{4}`
`J_{S}` = `\frac{\pi }{32}0.04^{4}`
`\mathbf{J_{S}}` = 2.513 x 10⁻⁷ m⁴
Step 3] Polar moment of inertia of hollow circle:
Polar moment of inertia of a hollow circle is given by,
`J_{H}` = `\frac{\pi }{32}[D_{\text{H(o)}}^{4}-D_{\text{H(i)}}^{4}]`
`J_{H}` = `\frac{\pi }{32}[0.06^{4}-0.047^{4}]`
`\mathbf{J_{H}}` = 7.932 x 10⁻⁷ m⁴
Step 4] Compare polar moment of inertia of solid and hollow shaft:
`\frac{J_{H}}{J_{S}}` = `\frac{7.932\times 10^{-7}}{2.513\times 10^{-7}}`
`\frac{J_{H}}{J_{S}}` = 3.156
| `\mathbf{J_{H} = 3.156 J_{S}}` |
Thus the hollow shaft has a polar moment of inertia equal to 3.156 times of polar moment of inertia of the solid shaft.