The term radius of gyration is used in both rotational dynamics and static loading. In the case of a rotating body, the radius of gyration illustrates the distribution of mass along the axis of rotation, whereas in static loading, the radius of gyration depicts the distribution of area around the axis.
Thus, in this article, we will go through each of them in detail.
Contents:
What is Radius of gyration (Rotational motion)?
The radius of gyration is defined as the distance from the axis of rotation to the point where the whole mass of a body is supposed to be concentrated which should give the same moment of inertia as that of the original shape.
The radius of gyration is denoted by the symbol ‘K’ or ‘`R_{G}`’.
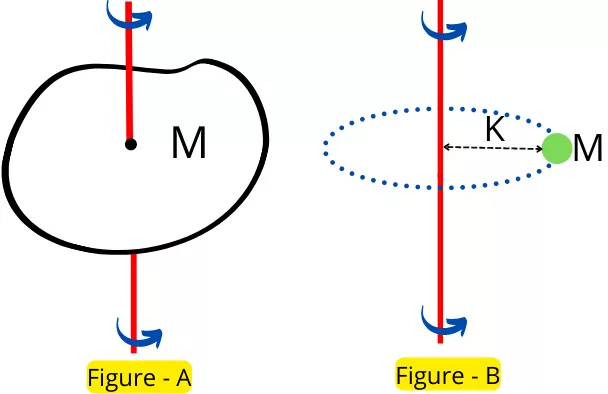
Figure-A shows the object of mass M rotating about the verticle axis and figure. B shows the mass of a whole body is concentrated at a distance of K from the axis of rotation.
As per the definition of the radius of gyration, the moment of inertia of the body shown in figure-A is equal to the moment of inertia of concentrated point mass (shown in figure B) about the same axis.
As per the condition of radius of gyration,
`I` = `I_{\text{Point mass}}`
`I` = `K^{2}`.M
Where,
K = Radius of gyration
In the SI system, the unit of the radius of gyration is ‘ meter (m)’ and in the FPS system, the unit is ‘Foot (Ft)’. The dimensional formula of the radius of gyration is [L¹M⁰T⁰].
What is Radius of gyration (Static loading)?
The radius of gyration is the distance from the centroidal axis to a point where the total area of the shape is assumed to be focused which gives the same moment of inertia as that of the original shape.
Mathematically it can be expressed as,
`I` = Moment of inertia of focused mass
`I` = `K^{2}`.A
Where,
K = Radius of gyration
A = Total area of cross-section
Radius of gyration equations:
For rotational motion:
The radius of gyration for the rotating object of mass M is given by,
| K = `\mathbf{\sqrt{\frac{I}{M}}}` |
Where,
I = Mass moment of inertia about axis of rotation
M = Mass of object
For the body consists of ‘n’ number of small particles of the same mass, the radius of gyration is given by,
| K = `\mathbf{\sqrt{\frac{r_{1}^{2}+r_{2}^{2}+\cdots + r_{n}^{2}}{n}}}` |
Where,
`r_{1},r_{2} \cdots r_{n}` = Distance of each particle from axis of rotation
n = Total number of particles
For static loading:
For the object under a static loading situation, the radius of gyration is given by,
| K = `\mathbf{\sqrt{\frac{I}{A}}}` |
Where,
I = 2ⁿᵈ moment of area of shape about the centroidal axis
A = Total area of cross-section
Polar radius of gyration:
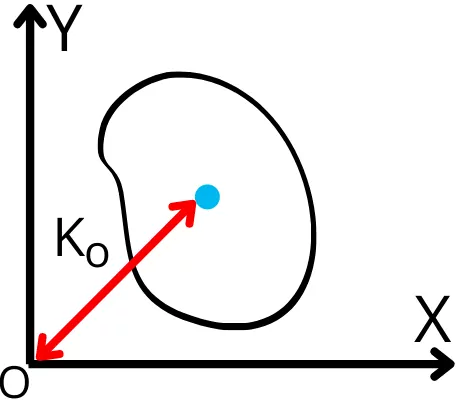
For the static loading, the polar radius of gyration can be calculated by using the following formula:-
`K_{o}` = `\sqrt{\frac{I_{o}}{A}}`
Where,
`I_{o}` = Polar moment of inertia about O
A = Total area of cross-section
Radius of gyration derivation (Rotational motion):
Consider a body of total mass M consists of ‘n’ number of small particles having of equal mass. (`m_{1}` = `m_{2}` = `m_{3}` = `m_{n}` = m).
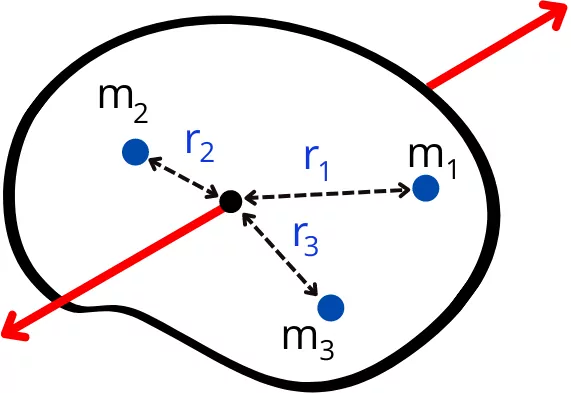
Thus the total mass of the body can be given by,
M = `m_{1}` + `m_{2}` + `m_{3}` + `\cdots ` + `m_{n}`
As the mass of all smaller particles is same.
∴ M = n x m
The total mass moment of inertia of all particles about the rotating axis is given by,
`I` = `\sum_{i=0}^{n} m_{i}r_{i}^{2}`
`I` = `m_{1}r_{1}^{2}` + `m_{2}r_{2}^{2}` + `m_{3}r_{3}^{2}` + `\cdots` + `m_{n}r_{n}^{2}`
`I` = `mr_{1}^{2}` + `mr_{2}^{2}` + `mr_{3}^{2}` + `\cdots` + `mr_{n}^{2}` ——-(∵ All particles has equal mass)
`I` = m(`r_{1}^{2}` + `r_{2}^{2}` + `r_{3}^{2}` + `\cdots` + `r_{n}^{2})`
As, m = M/n, then the equation can be written as,
`I` = `\frac{M}{n}`(`r_{1}^{2}` + `r_{2}^{2}` + `r_{3}^{2}` + `\cdots` + `r_{n}^{2})` – Equation [1]
Now as per the statement of radius of gyration,
If the whole mass of the body is supposed to be concentrated at a point that is away from the reference axis at a distance of K, then the moment of inertia of this concentrated mass about the reference axis is equal to the moment of inertia of the actual body at the same axis.
∴ `I_{\text{Concentrated mass}}` = `I`
M x K² = I
| K = `\sqrt{\frac{I}{M}}` —–Equation[2] |
By putting the value of equation-1 in the above equation,
K = `\sqrt{\frac{\frac{M}{n}(r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + \cdots + r_{n}^{2})}{M}}`
K = `\sqrt{\frac{r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + \cdots + r_{n}^{2}}{n}}`
| K = `\sqrt{\frac{\sum_{i=0}^{n}.r_{i}^{2}}{n}}` —–Equation [3] |
Therefore equation[2] and equation[3] give the radius of gyration of the body.
Importance of radius of gyration:
The following points shows that how radius of gyration is important for the analysis of the rotational motion and for the static loading analysis:-
1] The radius of gyration shows the distribution of mass from the axis of rotation.
If the radius of gyration is less then, it is concluded that the masses are closer to the axis of rotation and if the radius of gyration is high then it is concluded that the masses are located far from the axis of rotation.
2] The mass moment of inertia increases with the increase in radius of gyration and decreases with a decrease in radius of gyration.
3] In the case of structural analysis of columns, the radius of gyrations shows the distribution of the cross-section area from the axis.
How to calculate radius of gyration from moment of inertia?
Following are the methods to calculate the radius of gyration from two different moment of inertia:-
1] For rotational motion:
For the rotating mass with a mass moment of inertia of ‘Ⲓ’ and total mass of M, the radius of gyration is given by,
K = `\sqrt{\frac{I}{M}}`
2] For the static loading:
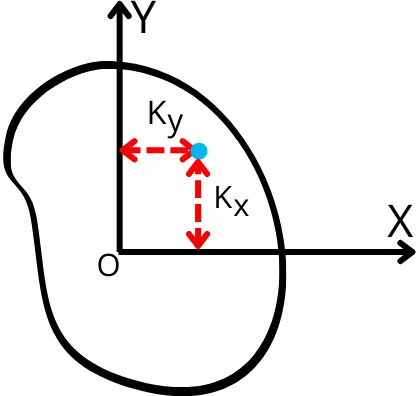
For the cross-section shown above, the radius of gyration about the x-axis is given by,
`K_{x}` = `\sqrt{\frac{I_{x}}{A}}`
Where,
`I_{x}` = Second moment of area about x-axis
A = Total area of cross-section
Similarly, the radius of gyration about the y-axis is given by,
`K_{y}` = `\sqrt{\frac{I_{y}}{A}}`
Where,
`I_{y}` = Second moment of area about y-axis
A = Total area of cross-section
Radius of gyration of different shapes (Rotational motion):
The equations of the radius of gyration for the different objects are as follows:-
1] Cylinder:-
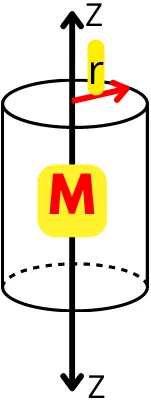
For the above cylinder of radius r and mass M, the mass moment of inertia about z-axis is given by,
`I_{z}` = `\frac{1}{2}Mr^{2}`
Thus, the radius of gyration about z-axis is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{M}}`
`K_{z}` = `\sqrt{\frac{\frac{1}{2}Mr^{2}}{M}}`
`K_{z}` = `\frac{r}{\sqrt{2}}`
| `\mathbf{K_{z}}` = `\mathbf{\frac{r}{\sqrt{2}}}` |
2] Sphere:-
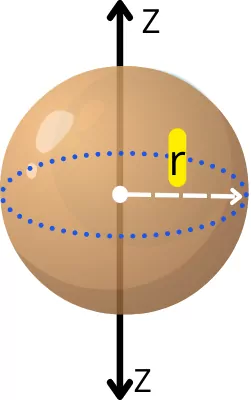
For the sphere of mass M and radius of r, the mass moment of inertia about the z-axis is given by,
`I_{z}` = `\frac{2}{5}Mr^{2}`
The radius of gyration about the z-axis is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{M}}`
`K_{z}` = `\sqrt{\frac{\frac{2}{5}Mr^{2}}{M}}`
| `\mathbf{K_{z}}` = `\mathbf{\sqrt{\frac{2}{5}}.r}` |
3] Thin rod:-
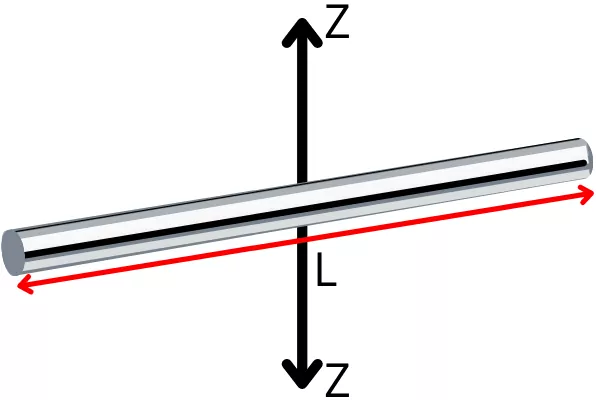
For the thin rod of mass M and length L, the mass moment of inertia about the z-axis is given by,
`I_{z}` = `\frac{ML^{2}}{12}`
The radius of gyration for thin rod about z-axis is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{M}}`
`K_{z}` = `\sqrt{\frac{\frac{ML^{2}}{12}}{M}}`
`K_{z}` = `\sqrt{\frac{L^{2}}{12}}`
| `\mathbf{K_{z}}` = `\mathbf{\frac{L}{2 \sqrt{3}}}` |
Radius of gyration of different shapes (Static loading):
The equations of the radius of gyration for different shapes are as follows:-
1] Radius of gyration of a circle-
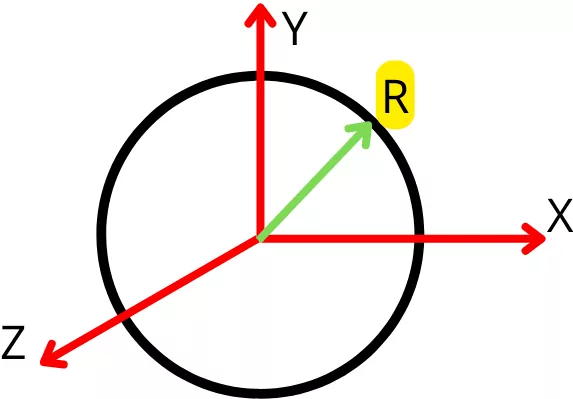
The 2ⁿᵈ moment of area about the x or y-axis is given by,
`I_{x}` = `I_{y}` = `\frac{\pi }{4}r^{4}`
Thus the radius of gyration about x or y axis is given by,
`K_{x}` = `K_{y}` = `\sqrt{\frac{I_{x}}{A}}` = `\sqrt{\frac{\frac{\pi }{4}r^{4}}{\pi r^{2}}}` = `\frac{r}{2}`
| `\mathbf{K_{x}}` = `\mathbf{K_{y}}` = `\mathbf{\frac{r}{2}}` |
The polar moment of inertia for the circle is given by,
`I_{z}` = `\frac{\pi }{2}r^{4}`
Thus the polar radius of gyration about z-axis is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{A}}` = `\sqrt{\frac{\frac{\pi }{2}r^{4}}{\pi r^{2}}}` = `\frac{r}{\sqrt{2}}`
`K_{z}` = `\frac{r}{\sqrt{2}}`
| `\mathbf{K_{z}}` = `\mathbf{\frac{r}{\sqrt{2}}}` |
2] Radius of gyration of a rectangle:-
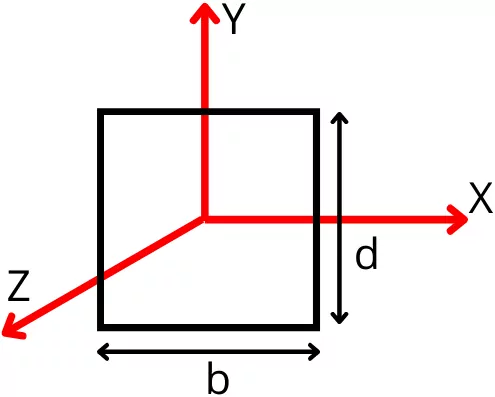
The 2ⁿᵈ moment of area about x-axis is given by,
`I_{x}` = `\frac{bd^{3}}{12}`
The radius of gyration about x-axis is given by,
`K_{x}` = `\sqrt{\frac{I_{x}}{A}}` = `\sqrt{\frac{\frac{bd^{3}}{12}}{bd}}` = `\sqrt{\frac{d^{2}}{12}}` = `\frac{d}{2\sqrt{3}}`
| `\mathbf{K_{x}}` = `\mathbf{\frac{d}{2\sqrt{3}}}` |
The 2ⁿᵈ moment of area about y-axis is given by,
`I_{y}` = `\frac{db^{3}}{12}`
The radius of gyration about the y-axis is given by,
`K_{y}` = `\sqrt{\frac{I_{y}}{A}}` = `\sqrt{\frac{\frac{db^{3}}{12}}{bd}}` = `\sqrt{\frac{b^{2}}{12}}` = `\frac{b}{2\sqrt{3}}`
| `\mathbf{K_{y}}` = `\mathbf{\frac{b}{2\sqrt{3}}}` |
The polar moment of inertia about z-axis is given by,
`I_{z}` = `\frac{bd^{3}}{12}` + `\frac{db^{3}}{12}`
The polar radius of gyration about z-axis is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{A}}` = `\sqrt{\frac{\frac{bd^{3}}{12}+\frac{db^{3}}{12}}{bd}}`
`K_{z}` = `\sqrt{\frac{d^{2}+b^{2}}{12}}`
| `\mathbf{K_{z}}` = `\mathbf{\frac{\sqrt{d^{2}+b^{2}}}{2 \sqrt{3}}}` |
Radius of gyration vs Centroid:
| Sr. No. | Centroid | Radius of gyration |
|---|---|---|
| 1 | It is the center of gravity of a plane lamina. | The radius of gyration is defined as the distance from the axis of rotation to the point where the whole mass/area of a body is supposed to be concentrated which gives the same moment of inertia as that of the original shape. |
| 2 | The position of centroid (x̄, ȳ) is given by, x̄ = `\frac{\int x.dA}{\int dA}` ȳ = `\frac{\int y.dA}{\int dA}` | The radius of gyration is given by, K = `\sqrt{\frac{I}{M}}` |
| 3 | The centroid is used in statics to analyze the structures under different loading situations. | The radius of gyration is used in rotational dynamics as well as in static structural analysis. |
Radius of gyration examples:
| 1] A cylinder of mass 10 kg and a radius of 0.2 m is rotating about its vertical centroid axis. Find the radius of gyration of the cylinder about the z-axis. |
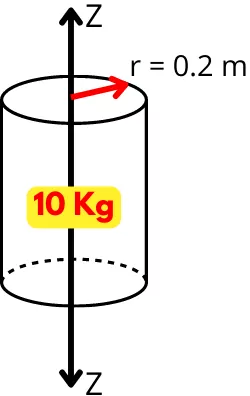
Given:
M = 10 Kg
r = 0.2 m
Solution:-
The mass moment of inertia about vertical axis is given by,
I = `\frac{1}{2}Mr^{2}`
I = `\frac{1}{2}` x 10 x 0.2²
| I = 0.2 Kg.m² |
Now the radius of gyration is given by,
K = `\sqrt{\frac{I}{M}}`
K = `\sqrt{\frac{0.2}{10}}`
| K = 0.141 m |
| 2] Find the radius of gyration of the following I-beam about a centroidal axis. |
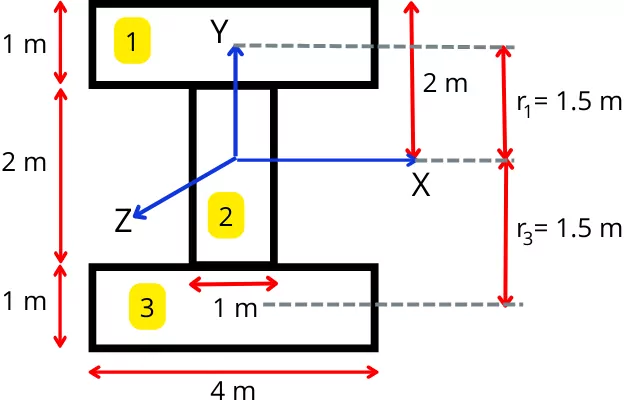
Solution:-
Step-1] Area of the I-section:-
`A_{1}` = 4 x 1 = 4 m²
`A_{2}` = 2 x1 = 2 m²
`A_{3}` = 4 x 1 = 4 m²
Total area of I beam is given by,
A = `A_{1} + A_{2} + A_{3}` = 4 +2 + 4 = 10 m²
Step-2] Polar moment of inertia about z-axis
The moment of inertia about x-axis is given by,
`I_{x}` = `I_{1x} + I_{2x} + I_{3x}`
By using parallel axis theorem for element 1 and 3, the equation becomes
`I_{x}` = `[I_{1}+A_{1}r_{1}^{2}]` + `[I_{2}]` + `[I_{3}+A_{3}r_{3}^{2}]`
`I_{x}` = `[\frac{4\times 1^{3}}{12}+4(1.5)^{2}]` + `[\frac{1\times 2^{3}}{12}]` + `[\frac{4\times 1^{3}}{12}+4(1.5)^{2}]`
| `I_{x}` = 19.33 m⁴ |
The moment of inertia about y-axis is given by,
`I_{y}` = `I_{1y} + I_{2y} + I_{3y}`
`I_{y}` = `[\frac{1\times 4^{3}}{12}]` + `[\frac{2\times 1^{3}}{12}]` + `[\frac{1\times 4^{3}}{12}]`
| `I_{y}` = 10.83 m⁴ |
The polar moment of inertia about z-axis is given by,
`I_{z}` = `I_{x} + I_{y}`
`I_{z}` = 19.33 + 10.83
| `I_{z}` = 30.16 m⁴ |
Step-2] Polar radius of gyration
The polar radius of gyration is given by,
`K_{z}` = `\sqrt{\frac{I_{z}}{A}}`
`K_{z}` = `\sqrt{\frac{30.16}{10}}`
| `K_{z}` = 1.736 m |
This is the polar radius of gyration about the z-axis.
FAQs:
-
Is radius of gyration scalar or vector?
The term radius of gyration is considered as the scalar quantity.
-
How do you find the radius of gyration?
The radius of gyration can be found by using the following formula,
K = √(𝙸/M)
Where,
𝙸 = Moment of inertia
M = Mass of the object -
What happens when radius of gyration of the body is large?
If the radius of gyration is large then the moment of inertia of the shape also becomes larger.
-
Is the radius of the gyration of a body a constant quantity Why?
No, the distribution of mass varies for the different axis of rotation, thus the radius of gyration also varies for the different axis of rotation.
-
Does the radius of gyration depends upon the speed of rotation of the body?
No, the speed of rotation of the body never affects the radius of gyration.