What is composite wall in heat transfer?
The composite wall is a wall that consists of a number of layers of different materials with varying thickness and thermal conductivity.
The layers of different conductive resistance are arranged in such a way that, the composite wall can achieve the required thermal resistance along with other requirements like lightweight, higher strength, durability, etc. Each layer is made up of different materials like wood, metals, refractory bricks, foam, glass wool, etc.
Therefore the composite wall helps us to meet different purposes along with thermal insulation.
Contents:
Purpose of composite wall:
It is difficult to attain the required amount of thermal resistance along with other important properties like strength, weight, etc by using a single material.
The composite wall is used to create the required amount of thermal resistance by arranging the number of layers of different materials.
Therefore by use of the composite wall, we can attend the required amount of thermal resistance along with other properties like high strength, lightweight, and compactness.
Application of composite wall:
The composite wall is generally used in the following applications:-
1) In cold places to avoid heat loss from buildings.
2) In industrial equipment to avoid heat loss.
3) In kitchen equipment like a thermos, Oven, etc.
Thermal resistance of composite wall:
The composite wall consists of a number of layers with different thermal resistances.
The conductive resistance offered by a single layer is given by,
`R=\frac{x}{A}`
Where,
x = Thickness of the layer
K = Thermal conductivity
A = Area of a cross-section perpendicular to the direction of flow
1) For a composite wall with layers arranged in series:
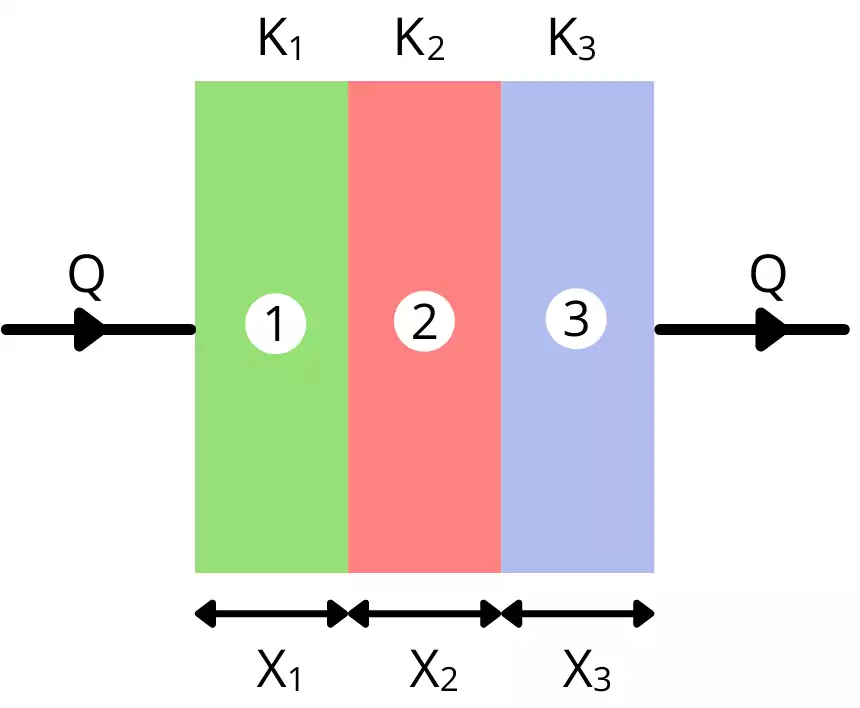
For n number of layers arranged in series, the total resistance is given by,
`R=R_{1}+R_{2}+R_{3}+\cdots R_{n}`
`R=\frac{x_{1}}{K_{1}A_{1}}+\frac{x_{2}}{K_{2}A_{2}}`+`\cdots \frac{x_{n}}{K_{n}A_{n}}`
2) For a composite wall with parallel arranged layers:
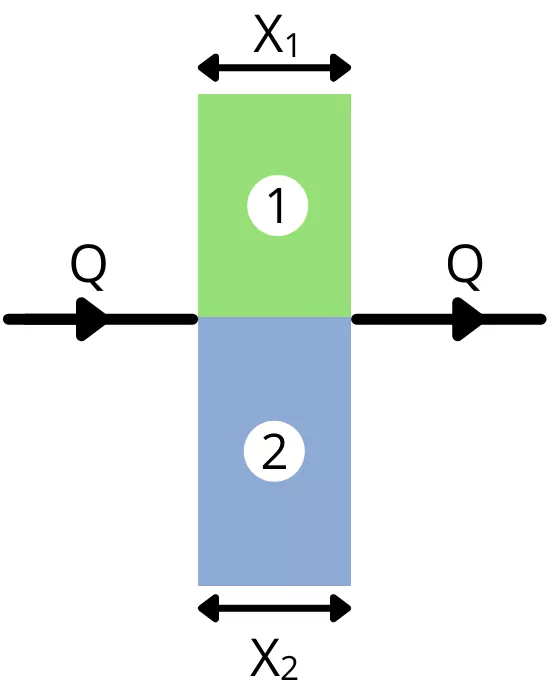
For n number of layers arranged in a parallel manner, the total resistance is given by,
`\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}+\cdots \frac{n}{R_{n}}}`
∴ R=`\frac{1}{\frac{x_{1}}{K_{1}A_{1}}+\frac{x_{2}}{K_{2}A_{2}}+\cdots \frac{x_{n}}{K_{n}A_{n}}}`
Thermal conductivity of composite wall:
For composite wall, the thermal conductivity is equivalent to the reciprocal of thermal resistance.
`\therefore K_{\text{composite wall}}=\frac{1}{R_{\text{composite wall}}}`
Read also: