Contents:
What is Wien’s displacement law?
Wien’s displacement law states that the wavelength with the peak emissive power is inversely proportional to the temperature of the black body. This law gives the relation between the temperature of the radiating black body and peak wavelength (wavelength with peak emissive power, `\lambda_{m}`).
The wavelength at which the black body emits maximum monochromatic emissive power is decreases with an increase in the absolute temperature (T) of the black body.
The German physicist Wilhelm Wien found a relationship between these two terms that says,
`\lambda_{m}\propto \frac{1}{T}`
`\lambda_{m} = \frac{B}{T}`
`T\lambda_{m} = B`
Where, B = 2.897 x 10⁻³ m.K
B is the proportionality constant and it has SI unit of m.K.
From the above equation, Wien’s displacement law can also be stated as the product of `\lambda_{m}` and T is constant.
Explanation:-
The bodies that are hotter than their surrounding radiates the energy to the surrounding with different wavelengths. This total radiating energy is distributed among these different wavelengths. Thus the energy associated with all wavelengths (Emissive power) varies from each other.
The wavelength that has maximum monochromatic emissive power is considered as `\lambda_{\text{max}}`.
The below figure shows the distribution of emissive power among different wavelengths emitted by the blackbody at constant temperature `T_{1}`.
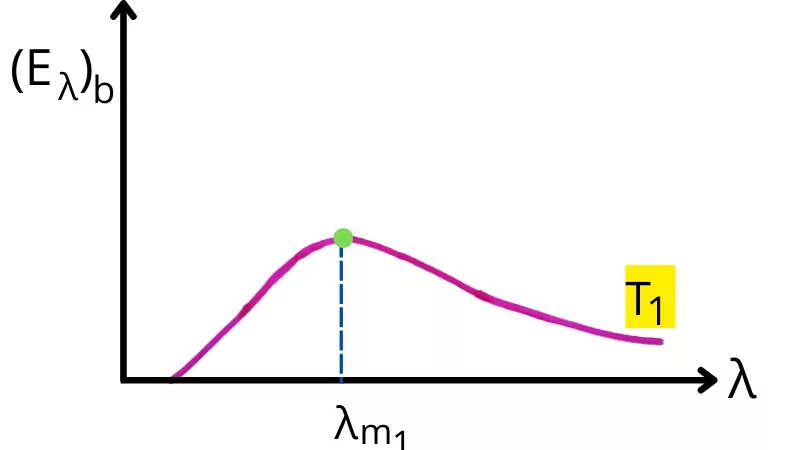
As shown in the above figure, at a particular point the value of the emissive power is maximum. The wavelength corresponding to the maximum emissive power is the `\lambda_{\text{max}}` or `\lambda_{m_{1}}`.
If we raise the temperature of the black body to `T_{2}`, then the graph becomes as follows,
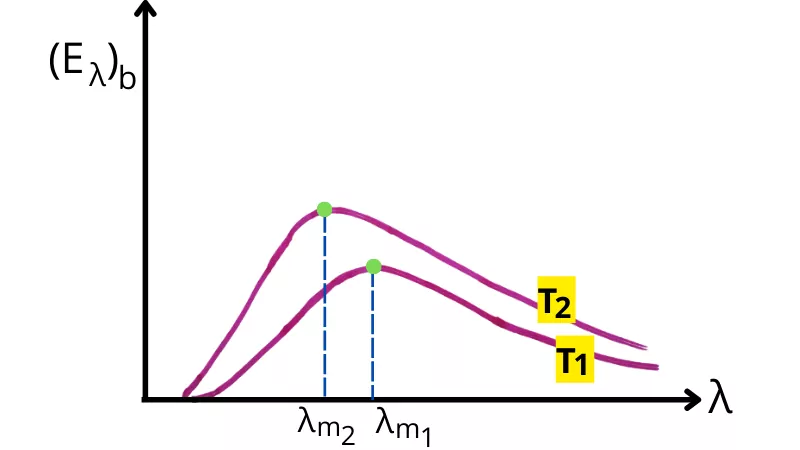
Thus at temperature `T_{2}` (where `T_{2}`>`T_{1}`), peak energy is emitted at a shorter wavelength `\lambda_{m_{2}}` (`\lambda_{m_{2}}`<`\lambda_{m_{1}}`).
Similarly, for the different temperatures, the curves of the emissive power distribution are as follows. (`T_{4}` > `T_{3}` > `T_{2}` > `T_{1}`)
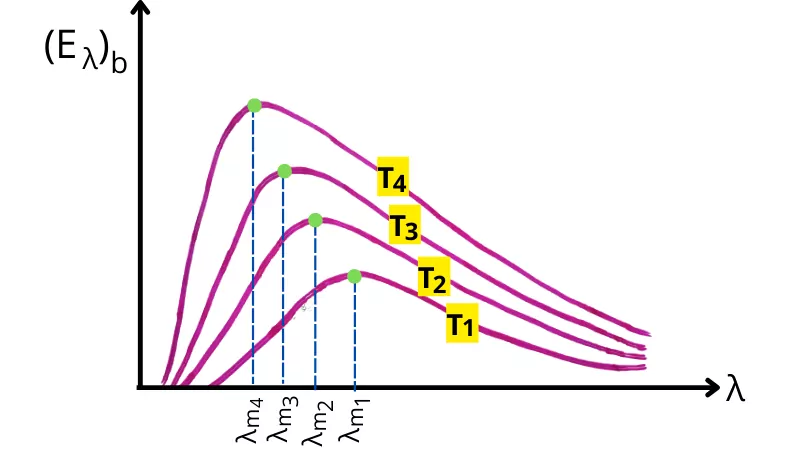
From the above graph, it is observed that as the temperature of the body increases, the wavelength with the peak emissive power displaces toward the right.
The physicist Wilhelm Wien found the relationship between the absolute temperature (T) and peak wavelength (`\lambda_{m}`) that is the product of T and its respective value of the `\lambda_{m}` remains constant.
`T\lambda_{m}` = Constant
Where,
`\lambda_{m}` = Wavelength at which maximum energy is emitted
T = Absolute temperature of black body
Wien’s displacement law derivation:
As per the plank’s law, the monochromatic emissive power of the blackbody is given by,
`(E_{\lambda})_{b}` = `\frac{C_{1}\lambda^{-5}}{e^{\frac{C_{2}}{\lambda T}}-1}`
Where,
`C_{1}` = 3.742 x `10^{8}` W.µm⁴/m²
`C_{2}` = 0.014388 mK
At constant temperature (T), the monochromatic emissive power of blackbody [`(E_{\lambda})_{b}`] becomes maximum when,
`\frac{d}{d\lambda}(E_{\lambda})_{b}` = 0
`\frac{d}{d\lambda}[\frac{C_{1}\lambda^{-5}}{e^{\frac{C_{2}}{\lambda T}}-1}]` = 0
By quotient rule of differentiation,
`\frac{[e^{\frac{C_{2}}{\lambda T}}-1]\frac{d}{d\lambda}(C_{1}\lambda^{-5})-(C_{1}\lambda^{-5})\frac{d}{d\lambda}[e^{\frac{C_{2}}{\lambda T}}-1]}{(e^{\frac{C_{2}}{\lambda T}}-1)^{2}}` = 0
`-5[e^{\frac{C_{2}}{\lambda T}}-1](C_{1}\lambda^{-6})` – `(C_{1}\lambda^{-5})[e^{\frac{C_{2}}{\lambda T}}.\frac{C_{2}}{T}(-\frac{1}{\lambda^{2}})]` = 0
`-5(C_{1}\lambda^{-6})[e^{\frac{C_{2}}{\lambda T}}]` + `5(C_{1}\lambda^{-6})` + `\frac{C_{1}C_{2}\lambda^{-6}}{\lambdaT}.e^{\frac{C_{2}}{\lambda T}}` = 0
`5C_{1}\lambda^{-6}[-e^{\frac{C_{2}}{\lambda T}}` + 1 + `(\frac{1}{5})(\frac{C_{2}}{\lambda T}).e^{\frac{C_{2}}{\lambda T}}]` = 0
`-e^{\frac{C_{2}}{\lambda T}}` + 1 + `\frac{1}{5}(\frac{C_{2}}{\lambda T}).e^{\frac{C_{2}}{\lambda T}}` = 0
Consider `\frac{C_{2}}{\lambda T}` = x, thus the above equation become,
`-e^{x}` + 1 + `\frac{x}{5}e^{x}` = 0
`(\frac{x}{5}-1)e^{x}` + 1 = 0
Solving the equation by trial and error method, we get
x = 4.965
∴ `\frac{C_{2}}{\lambda T}` = 4.965 —–[As x = `\frac{C_{2}}{\lambda T}` assumed]
At maximum value of `(E_{\lambda})_{b}`, `\lambda = \lambda_{\text{max}}=\lambda_{m}`
∴ `\frac{C_{2}}{\lambda_{m} T}` = 4.965
`\lambda_{m} T` = `\frac{C_{2}}{4.965}`
Putting value of `C_{2}` in above equation,
`\lambda_{m} T` = `\frac{0.014388}{4.965}`
| `\lambda_{m} T` = 2.897 x 10⁻³ m.K |
Significance of wien’s displacement law:
This law has following significances:-
- The law gives the relation between the peak wavelength emitted and the temperature of the blackbody.
- It is easy to find the approximate temperature of hotter bodies by knowing the peak wavelength emitted by the body.
- It implies that black bodies emitting peak emissive power at lower wavelengths are hotter than black bodies emitting peak emissive power at higher wavelengths.
Application:
Following are the applications of the Wien’s displacement law:-
1] Finding the approximate temperature of the stars:
The wien’s displacement law helps to find the approximate temperature of the stars. To find the approximate temperature, it is necessary to know the peak wavelength emitted by the star.
Example:- The peak wavelength emitted by the sun is 5 x 10⁻⁷ m. Thus the temperature of the sun can be calculated as follows,
`\lambda_{m} T` = 2.897 x 10⁻³
(5 x 10⁻⁷) x T = 2.897 x 10⁻³
T = 5794 K
T ≈ 5800 K
Thus in this way, it is easy to find the approximate temperature of the stars situated at a too far distance.
2] Incandescent bulb:
An incandescent bulb has a filament that is heated to a higher temperature to provide a spectrum of light.
The Wien’s displacement law helps to determine the relation between the temperature of the bulb and the wavelength of the required spectrum of light.
If the temperature of the filament is lower then it produces a reddish peak wavelength and as the temperature of the filament increases, the peak wavelength moves toward the bluish region of the visible spectrum (wavelength decreases).
Wien’s displacement law solved examples:
| 1. Consider the earth is at a temperature of 288 K. Find the peak wavelength of energy emitted by the earth. |
Given:
T = 288 K
Solution:-
By using wien’s displament law, the peak wavelength of the energy emitted from the earth is given by,
`\lambda_{m} T` = 2.897 x 10⁻³
`\lambda_{m}` x 288 = 2.897 x 10⁻³
`\lambda_{m}` = 1.005 x 10⁻⁵ m
Thus the earth is radiating the energy with a peak wavelength of 1.005 x 10⁻⁵ m.
| 2. A star emits radiation with a peak wavelength of 10⁻⁶ m. Find the approximate temperature of the star. |
Given:
`\lambda_{m}` = 10⁻⁶ m
Solution:-
Using wien’s displacement law,
`\lambda_{m} T` = 2.897 x 10⁻³
10⁻⁶ x T = 2.897 x 10⁻³
T = 2897 K
Thus the approximate temperature of the star is 2897 K.
FAQs:
-
What is the difference between Stefan Boltzmann law and Wien’s law?
The Stefan Boltzmann law gives the relation between the temperature and emissive power of the black body whereas the Wien’s displacement law gives the relation between the temperature and the peak wavelength emitted by the black body.
-
What are the limitations of Wien’s displacement law?
The wien’s displacement law gives inaccurate predictions at the higher wavelength and at the lower temperature.
-
Why is Wien’s law important?
The wien’s law provides the relation between the temperature of the black body and the wavelength at which the black body emits the peak energy.
-
What is the dimensional formula of Wien’s constant?
The dimensional formula of the Wien’s constant is [M¹ K¹].
We hope that this article has answered many of your questions about Wien’s displacement law. If you enjoyed this post, you should read our other articles about heat transfer.
Related articles: