What is shape factor in radiation?
Shape factor is the fraction of radiation energy radiated by one surface which is incident on another surface when both surfaces are placed in a non-absorbing medium.
The shape factor is denoted by the symbol Fij, where i indicates radiating surface and j indicates receiving surface.
That is for the two bodies 1 and 2, if the energy is radiated from 1st surface to 2nd surface, then the shape factor for this energy transfer is indicated as `F_{1-2}`.
Similarly, for the fraction of energy radiated from the 2nd surface to the 1st surface, the shape factor is given by `F_{2-1}`.
The shape factor is also known as the surface factor, configuration factor, or view factor.
In this article, we’re going to discuss:
- What is the purpose of shape factor?
- Basic considerations in shape factor:
- Shape factor equations:
- Numerical on shape factor:
What is the purpose of shape factor?
The shape factor helps to find the fraction of radiant energy emitted by one surface which is received by another surface.
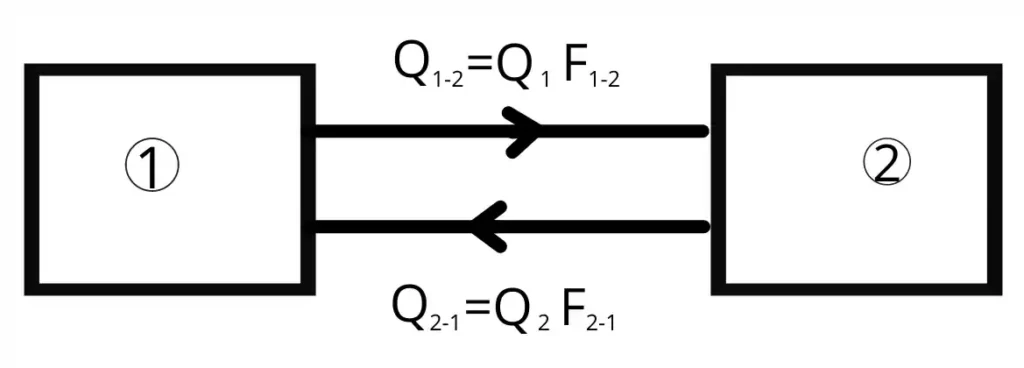
Example:- Consider two surfaces radiating energy Q1 and Q2 respectively.
In this case, the energy transferred from the surface 1st to 2nd surface is given by,
`Q_{1-2}=F_{1-2}.Q_{1}`
Where `Q_{1}=\sigma A_{1}T_{1}^{4}`
The radiation energy transferred from the 2nd surface to the 1st surface is given by,
`Q_{2-1}=F_{2-1}.Q_{2}`
Where `Q_{2}=\sigma A_{2}T_{2}^{4}`
Basic considerations in shape factor:
1) For flat surfaces:
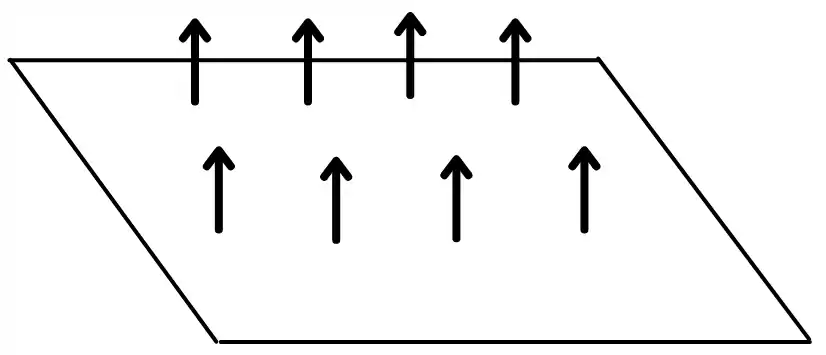
The flat surface never radiates a fraction of energy of its own surface. Therefore the view factor for such a surface is zero.
`F_{1-1}= 0`
2) For concave surface:
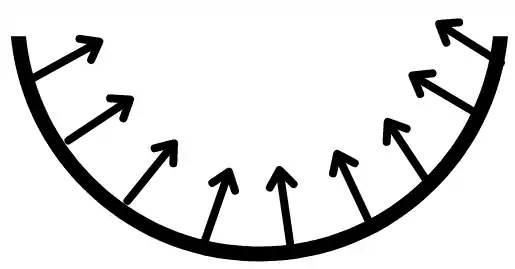
The concave surface can radiate some part of energy on its own surface. Therefore fraction of energy radiated by the surface on itself is given by shape factor `F_{1-1}`.
Therefore for the concave surface, the shape factor `F_{1-1}` is not equal to zero.
`F_{1-1}≠ 0`
3) For convex surface:
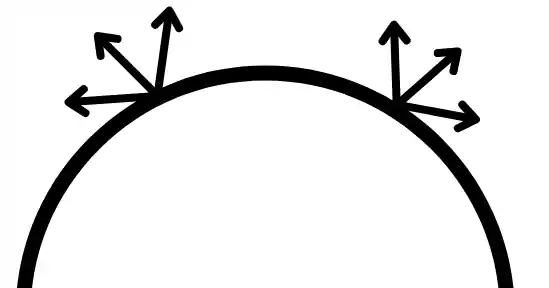
The convex surface never radiate fraction of energy on its own surface. Therefore for convex surface shape factor `F_{1-1}` is zero.
`F_{1-1}= 0`
Shape factor equations:
There are two theorems that state the relation between shape factors for enclosure surfaces.
A) Reciprocity theorem:
For the two surfaces, 1st and 2nd with surface area A1 and A2 respectively, the equation of reciprocity theorem is given by,
`A_{1}F_{1-2}=A_{2}F_{2-1}`
B) Principle of conservation:
If the enclosure consists of n number of surfaces and if one surface out of them is radiating energy then,
The summation of energy incidents on each surface is equal to the total energy radiated by that single surface.
Example:- As shown in the below figure the enclosures consist of four surfaces.
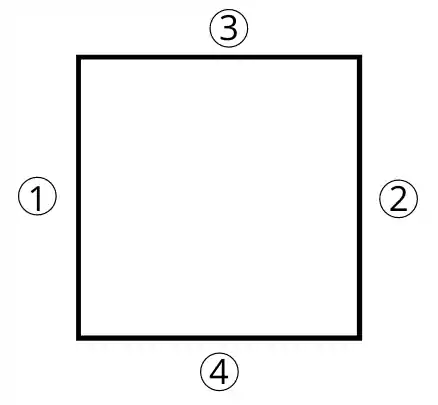
If surface 1st is radiating the energy then the summation of all shape factors associated with surface 1st is equal to 1.
`F_{1-1}+F_{1-2}+F_{1-3}+F_{1-4}=1`
The principle is the same for other radiating surfaces,
`F_{2-1}+F_{2-2}+F_{2-3}+F_{2-4}=0`
`F_{3-1}+F_{3-2}+F_{3-3}+F_{3-4}=0`
`F_{4-1}+F_{4-2}+F_{4-3}+F_{4-4}=0`
Numerical on shape factor:
- For the following figure calculates all the shape factors associated with two concentric cylinders.
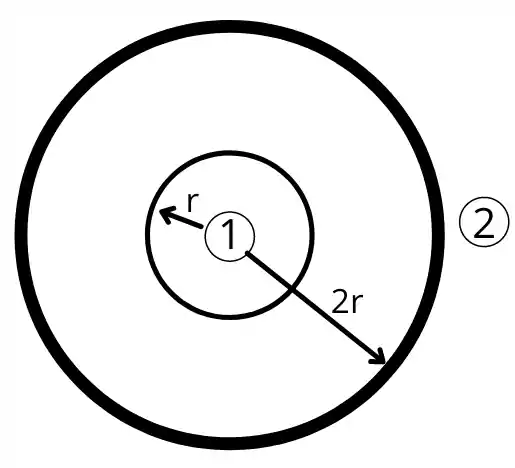
As Cylinder one has a convex radiating surface, therefore,
`F_{1-1}=0`
Now by using principle of conservation for surface-1,
`F_{1-1}+F_{1-2}=1`
`0+F_{1-2}=1`
`F_{1-2}=1`
Now by using reciprocity theorem between surface 1st and 2nd,
`A_{1}F_{1-2}=A_{2}F_{2-1}`
Where, A1 = 2πrL and A2 = 2π(2r)L = 4πrL
(2πrL).(1) = 4πrL x `F_{2-1}`
`F_{2-1}=0.5`
Now by using the principle of conservation for surface 2nd,
`F_{2-1}+F_{2-2}=1`
`0.5+F_{2-2}=1`
`F_{2-2}=0.5`
Therefore shape factors are,
`F_{1-1}=0`
`F_{1-2}=1`
`F_{2-1}=0.5`
`F_{2-2}=0.5`
Read also: