Contents:
What is radiation intensity?
The radiation intensity is defined as the amount of energy emitted per unit solid angle by per unit area of the radiating surface.
The radiation intensity is denoted by symbol I.
| ∴ Radiation intensity `I= \frac{E}{A \omega} ` |
Where, E is emissive power and ω is the solid angle.
The radiation intensity is also known as the intensity of Radiation.
Radiation intensity unit:
In SI system:
The SI unit for emissive power is W and the SI unit for the area and solid angle is m² and steradian respectively.
Therefore unit of radiation intensity is,
`I= \frac{E}{A \omega} = \frac{W}{m^{2}.sr} `
∴ The SI unit of solid angle is W/m².sr
In FPS system:
The FPS unit for emissive power is Btu/hr and the FPS unit for the area and solid angle is ft² and steradian respectively.
Therefore unit of radiation intensity is,
`I= \frac{E}{A \omega} = \frac{Btu}{hr.ft².sr}`
∴ The FPS unit of solid angle is Btu/hr.ft².sr
Radiation intensity formula:
The radiation intensity in the normal direction is given by,
`In=\frac{E}{\pi }`
Where, E= Emissive power
For the direction inclined at the angle of ψ, the radiation intensity is given by,
`I=In\times cos\Psi `
Derivation for radiation intensity:
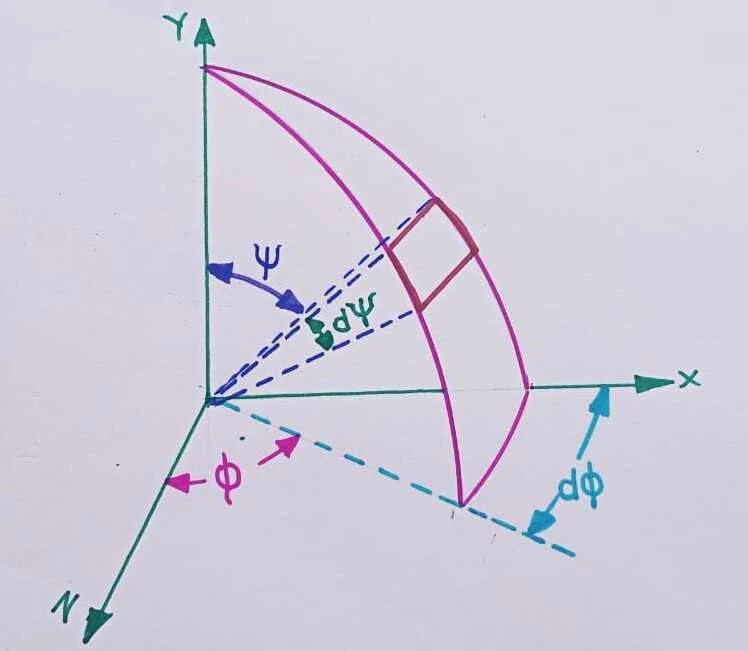
By the definition of radiation intensity, we get,
`I=\frac{dE}{d\omega } `
`dE=I\times d\omega `
By integrating both sides,
`E=\int I\times d\omega `
The elemental solid angle dω is given by,
`d\omega =sin\Psi .d\Psi. d\phi `
Therefore put the value of dω and integrate the equation
`E=\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{2}}i.sin\Psi .d\Psi. d\phi `
For the solid angle of π,
The zenith angle ψ varies from 0 to 2π radian.
The azimuth angle ϕ varies from 0 to π/2 radian.
By lambert cosine law,
`i=i_{n}.cos\Psi `
Where `i_{n}` is the intensity in the normal direction.
By putting lambert cosine law,
`E=\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{2}}i_{n}.cos\Psi.sin\Psi .d\Psi. d\phi `
Solving the above integration we get,
`E=i_{n}\pi `
| `i_{n}=\frac{E}{\pi }` |
This is the required equation for radiation intensity in the normal direction.
Solid angle (ω):
A solid angle is the conical portion of a sphere with the vertex of the cone coinciding with the center of the sphere.
The solid angle is calculated by the ratio of surface area covered by the cone to the square of the radius of the sphere.
∴ Solid angle (ω) = `\frac{A}{r_{sphere}^{2}}`
For hemispherical surface, the solid angle is given by,
`A=2\pi r^{2}`
∴ Solid angle (ω)= `\frac{2\pi r^{2}}{r^{2}}=2\pi `
For spherical surface, the solid angle is given by,
`A=4\pi r^{2}`
| Solid angle (ω)= `\frac{4\pi r^{2}}{r^{2}}=4\pi ` |
The unit of solid angle is steradian.
Read also: