What is the Carnot cycle?
The Carnot cycle is an ideal cycle that consists of four reversible processes, out of them two are reversible adiabatic processes & remaining two are reversible isothermal processes.
This cycle was invented by french scientist Nicolas leonard sadi carnot in 1824.
Carnot cycle has maximum efficiency for engines working between two different temperatures, TH (heat source temperature) and TL (Sink temperature). It means that, the efficiency of any heat engine does not exceed Carnot’s efficiency.
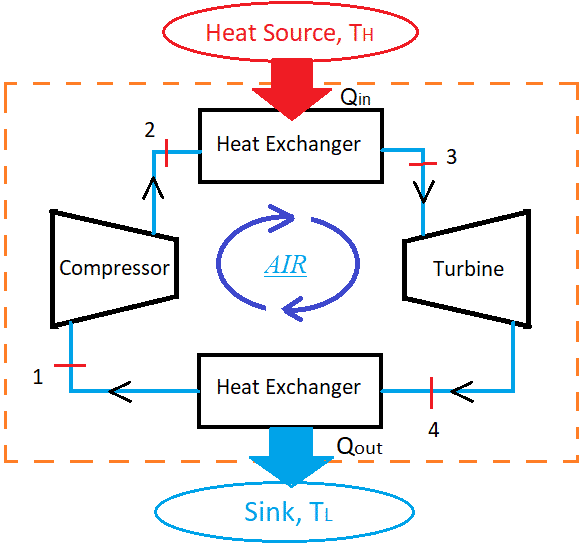
In the Carnot cycle, processes are non-flow processes, which means that this cycle never exchanges mass with the surrounding. Thus, it uses heat exchangers for the heat transfer.
Contents:
Processes in Carnot cycle:
The below figure shows all processes on PV and TS plot.
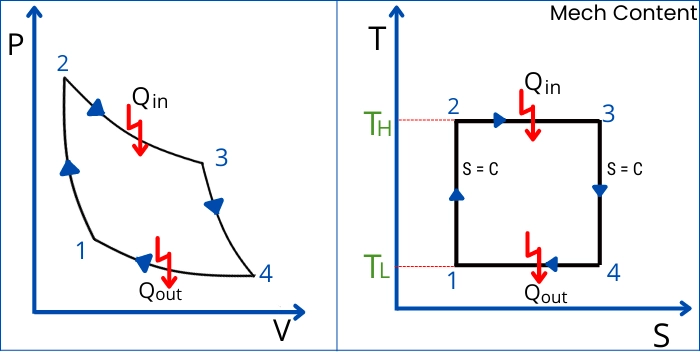
This cycle consists of following four processes:
Process 1-2 (Reversible adiabatic compression): During this process, air is compressed in an adiabatic manner.
Process 2-3 (Reversible Isothermal heat addition): This process is also known as Reversible Isothermal expansion. During this process, heat is added to the air by an external heat source without changing its temperature.
Process 3-4 (Reversible adiabatic expansion): This process indicates the adiabatic expansion of the air from state 3 to 4.
Process 4-1 Reversible isothermal compression: (Also known as Reversible Isothermal heat rejection): During this process, air rejects heat isothermally, to the external heat sink at temperature TL.
Also read: Why Carnot cycle cannot be realized in practical?
Carnot cycle assumptions:
The assumptions considered in Carnot cycle are as follows:
- Working fluid is air.
- Air is considered an ideal gas.
- No internal heat generation, It means that heat is added & rejected externally.
Analysis of Carnot cycle:
Let’s analyze each of the process thermodynamically.
Process (1-2):
It is a reversible adiabatic compression process. Here temperature of air increases from T1 to T2 (that is TL to TH).
Hence, internal energy also increases, which is given by,
du1-2 =CV(T2 – T1)
As T2 = TH and T1 = TL
`\therefore \mathbf{du_{1-2}=C_{V}(T_{H}- T_{L})}`
For adiabatic process,
`\mathbf{Q_{1-2}= 0}`
Now by the first law of thermodynamics,
`Q_{1-2}=du_{1-2}+W_{1-2}`
`0=C_{V}(T_{H}- T_{L})+W_{1-2}`
`\mathbf{W_{1-2}=C_{V}(T_{L}- T_{H})}`
Process (2-3):
It is a reversible isothermal expansion process.
For the isothermal process, the change in internal energy is zero,
`\therefore \mathbf{du_{2-3}=0}`
And work done for an isothermal process 2-3 is given by,
`W_{2-3}= RT_{2} ln frac{V_{3}}{V_{2}}`
But as T2 = TH,
∴`\mathbf{W_{2-3}= RT_{H} ln frac{V_{3}}{V_{2}}}`
Now, by the first law of thermodynamics,
`Q_{2-3}=du_{2-3}+W_{2-3}`
`Q_{2-3}=0+RT_{H} ln frac{V_{3}}{V_{2}}`
`\mathbf{Q_{2-3}=RT_{H} ln frac{V_{3}}{V_{2}}}`
Process (3-4):
It is a reversible adiabatic expansion process.
For adiabatic process,
`\mathbf{Q_{3-4}=0}`
In this process, the temperature of the air decreases from T3 to T4 (that is TH to TL).
Hence, the change in internal energy du3-4 is given by,
`du_{3-4}=C_{V}( T_{4}-T_{3})`
As T3 = TH and T4 = TL
`\therefore \mathbf{du_{3-4}=C_{V}( T_{L}-T_{H})}`
Now by the first law of thermodynamics,
`Q_{3-4}=du_{3-4}+W_{3-4}`
`0=C_{V}(T_{L}-T_{H}) + W_{3-4}`
`\mathbf{W_{3-4}=C_{V}(T_{H} -T_{L})}`
Process (4-1):
It is reversible Isothermal compression or heat rejection process.
In this process, as the temperature remains constant, thus the internal energy is not changing.
∴`\mathbf{du_{4-1}=0}`
For this isothermal process, work done is given by,
`W_{4-1}=RT_{4}ln frac{V_{1}}{V_{4}}`
But as T4 = TL,
∴`\mathbf{W_{4-1}=RT_{L}ln frac{V_{1}}{V_{4}}}`
By the first law of thermodynamics,
`Q_{4-1}=du_{4-1}+W_{4-1}`
`Q_{4-1}=0+RT_{L}ln frac{V_{1}}{V_{4}}`
`\mathbf{Q_{4-1}=RT_{L}ln frac{V_{1}}{V_{4}}}`
All parameters are summarized in below table:

Work done in Carnot cycle:
The net work done for the closed cycle is given by,
`W_{\text{Net}}=Q_{\text{Net}}`
`\thereforeW_{\text{Net}}=Q_{\text{In}}+Q_{\text{out}}`
`W_{\text{Net}}=Q_{2-3}+ Q_{4-1}`
`W_{\text{Net}}=RT_{H}ln(\frac{V_{3}}{V_{2}})+RT_{L}ln(\frac{V_{1}}{V_{4}})`
`W_{\text{Net}}=RT_{H}ln(\frac{V_{3}}{V_{2}})-RT_{L}ln(\frac{V_{4}}{V_{1}})`
But `\frac{V_{4}}{V_{1}}=\frac{V_{3}}{V_{2}}`
`\therefore W_{\text{Net}}=RT_{H}.ln(\frac{V_{3}}{V_{2}})-RT_{L}.ln(\frac{V_{3}}{V_{2}})`
`W_{\text{Net}}=R(T_{H}-T_{L})ln(\frac{V_{3}}{V_{2}})`
Carnot cycle efficiency derivation:
The thermal efficiency of the Carnot cycle is the highest efficiency of any heat engine working between two temperatures TL and TH (TH>TL).
No heat engine gives higher efficiency than a Carnot heat engine.
The heat supplied QIn during the process 2-3 is given by,
`Q_{\text{In}}= Q_{2-3}=RT_{H}ln(\frac{V_{3}}{V_{2}})`
The heat rejected during the process 4-1 is given by,
`Q_{\text{Out}}= Q_{4-1}=RT_{L}ln(\frac{V_{1}}{V_{4}})`
The net heat transfer is given by,
`Q_{\text{Net}}=Q_{\text{In}}+Q_{\text{Out}}`
`Q_{\text{Net}}=RT_{H}ln(\frac{V_{3}}{V_{2}})+RT_{L}ln(\frac{V_{1}}{V_{4}})`
`Q_{\text{Net}}=RT_{H}ln(\frac{V_{3}}{V_{2}})-RT_{L}ln(\frac{V_{4}}{V_{1}})`
Now the efficiency is given by,
`\eta _{th}= frac{W_{\text{Net}}}{Q_{\text{In}}}`
For the cycle, WNet = QNet
`\therefore \eta _{th}= frac{Q_{\text{Net}}}{Q_{\text{In}}}`
`\eta _{th}= frac{RT_{H}ln(\frac{V_{3}}{V_{2}})-RT_{L}ln(\frac{V_{4}}{V_{1}})}{RT_{H}ln(\frac{V_{3}}{V_{2}})}`
Since `frac{V_{4}}{V_{1}}= \frac{V_{3}}{V_{2}}`
`\therefore \eta_{th}= frac{RT_{H}ln(\frac{V_{3}}{V_{2}})-RT_{L}ln(\frac{V_{3}}{V_{2}})}{RT_{H}ln(\frac{V_{3}}{V_{2}})}`
`\therefore \eta_{th}=\frac{T_{H}-T_{L}}{T_{H}}`
`\therefore \eta_{th}=1-\frac{T_{L}}{T_{H}}`
This is the equation to find the efficiency of the Carnot cycle working between the temperature TH and TL.
Solved Examples:
1] Find the maximum efficiency of the heat engine working between source temperature 400 kelvin & Sink temperature 350 Kelvin.
Given:
TH =400 K
TL =350 K
Solution:
The maximum efficiency attained by any heat engine is equal to the efficiency of a Carnot cycle which is given by,
`\eta_{th} =1-\frac{T_{L}}{T_{H}}`
`\eta_{th} =1-\frac{350}{400}`
`\eta_{th}` = 0.125 OR 12.5 %
It shows that any engine working between these two temperatures has maximum attainable efficiency of 12.5%.
2] A Carnot cycle engine working between temperatures 300K and 400K gives a net work output of 70 Watt. Find the amount of heat supplied to the Carnot engine.
Given:
TH = 400 K
TL = 300 K
WNet = 70 watt
Solution:
The Carnot engine’s efficiency is given by,
`\eta_{th} =1-\frac{T_{L}}{T_{H}}`
`\eta_{th} =1-\frac{300}{400}`
`\eta_{th}=0.25`
The heat engine’s thermal efficiency is determined by,
`\eta _{th}= frac{W_{\text{Net}}}{Q_{\text{In}}}`
`0.25= frac{70}{Q_{\text{In}}}`
`\mathbf{Q_{\text{In}}=280\ \text{Watt}}`
FAQs:
-
What factors influence the efficiency of a Carnot cycle?
The efficiency of the Carnot cycle is influenced by the absolute temperatures of the source and sink (T🇭, T🇱).
-
Which thermodynamic cycle is the most efficient?
The Carnot cycle provides maximum efficiency among all cycles working between the same source and sink temperatures.
Read also: