The most common methods to improve gas turbine performance are regeneration, intercooler, and reheating. In this post, we will discuss the method of reheating in the gas turbine and how it affects the performance of the gas turbine.
Contents:
What is Reheating in gas turbine?
Reheating in gas turbine is the method of extracting extra work output from the gas turbine in which the exhaust gas from the main turbine (High-pressure turbine) is heated and then expanded further into the next low-pressure turbine.
The exhaust gases leaving the combustion chamber (CC in the figure), still contain a specific portion of air that did not participate in the combustion process. Thus during reheating this air is utilized by adding extra fuel into the reheater to again raise the temperature of the gases.
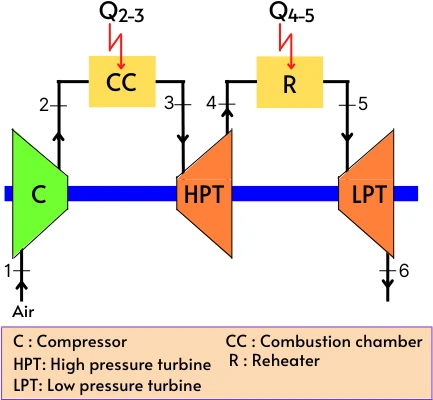
As shown in the above figure, in this method, the expansion of the gases is carried out in two turbines mounted on the same shaft and the reheating is done in between these two turbines.
After the expansion in the high-pressure turbine up to the intermediate pressure, the gases enter into the reheater. Here the extra fuel is burned along with the portion of air present in the exhaust gases.
The purpose of a reheater is to raise the temperature of the gases up to the maximum temperature.
The gases leaving the reheater are then fully expanded into the low-pressure turbine.
Effects of reheating in gas turbine:
The following are some effects of reheating on the gas turbine:-
- The reheating raises the temperature of the turbine exhaust.
- It helps to increase the work output from the gas turbine.
- Only reheating does not raise or lower the efficiency of the gas turbine as it also takes extra heat input for reheating.
- It also increases the amount of heat rejected from the turbine.
PV and TS diagram:
The below figure shows, the PV and TS diagram for the gas turbine cycle with reheating.
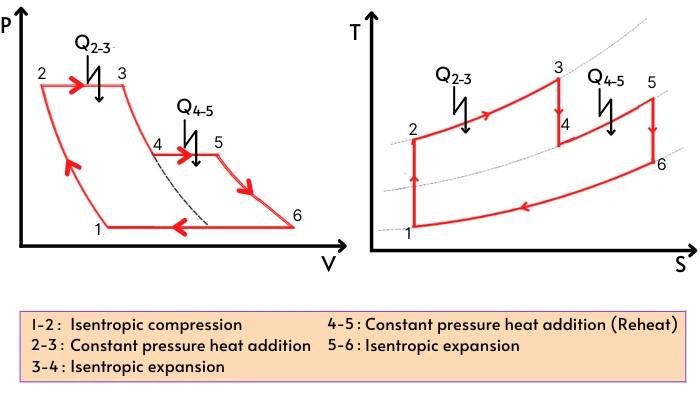
As shown in the above figure, during processes 3-4, the gases expand in the high-pressure turbine from compressor pressure P1 to intermediate pressure Pi.
To obtain the maximum work, the intermediate pressure (reheating pressure) is given by,
`P_{i}=\sqrt{P_{1}.P_{2}}`
Process 4-5 indicate the constant pressure heat addition, or reheating process.
The ideal reheating says that the temperature of the gas entering the low-pressure turbine should be equal to the temperature of the air entering the high-pressure turbine.
`T_{5}=T_{3}`
Efficiency:
The reheating can increase or decrease the efficiency of the gas turbine.
The total work done by the turbines is given by,
`W_{\text{turbine}}=W_{\text{HP turbine}}+W_{\text{LP turbine}}`
`W_{\text{turbine}}=W_{3-4}+W_{5-6}`
`W_{\text{turbine}}=Cp(T_{3}-T_{4})+Cp(T_{5}-T_{6})`
The net work done from the gas turbine is given by.
`W_{\text{Net}}=W_{\text{turbine}}-W_{\text{compressor}}`
`W_{\text{Net}}=W_{\text{turbine}}-(Cp(T_{2}-T_{1}))`
`W_{\text{Net}}=(Cp(T_{3}-T_{4})+Cp(T_{5}-T_{6}))-(Cp(T_{2}-T_{1}))`
The total heat supplied to the gas turbine is given by,
`Q_{\text{in}}=Q_{2-3}+Q_{4-5}`
`Q_{\text{in}}=Cp(T_{3}-T_{2})+Cp(T_{5} – T_{4})`
The efficiency of the gas turbine with the reheating is given by,
`\eta_{th}=\frac{W_{\text{net}}}{Q_{\text{in}}}`
`\eta_{th}=\frac{Cp(T_{3}-T_{4})+Cp(T_{5}-T_{6})-Cp(T_{2}-T_{1})}{Cp(T_{3}-T_{2})+Cp(T_{5} – T_{4})}`
`\mathbf{\eta_{th} = \frac{(T_{3}-T_{4})+(T_{5}-T_{6})-(T_{2}-T_{1})}{(T_{3}-T_{2})+(T_{5} – T_{4})}}`
Advantages of reheating in a gas turbine:
The reheating in gas turbine power plant has the following advantages:-
- Increases the turbine work
- Increases the net-work output
- Its combination with an intercooler increases thermal efficiency.
Numerical:
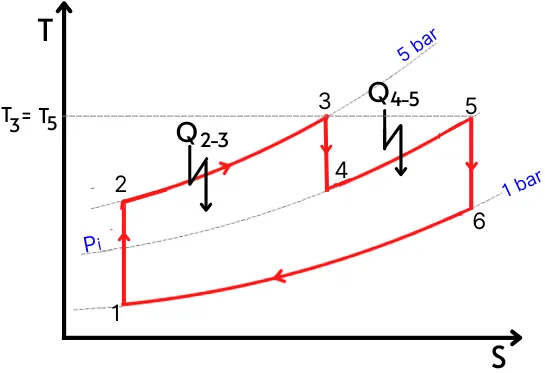
In the gas turbine, the air at 1 bar and 305 K is compressed to 5 bar. In the primary combustion chamber, 300 KJ/Kg heat is added to the air. If the turbine uses a reheater, find the maximum work output from the gas turbine. (Assume `\gamma` = 1.4 and `C_{P}` = 1.005 KJ/Kg)
Given:
`P_{1}=P_{6}` = 1 bar
`T_{1}` = 305 K
`P_{2}=P_{3}` = 5 bar
`q_{2-3}` = 300 KJ/Kg
Solution:-
Compressor 1-2:
For isentropic compression, the relation between the pressure and temperature is given by,
`\frac{T_{2}}{T_{1}}=(\frac{P_{2}}{P_{1}})^{\frac{\gamma-1}{\gamma}}`
`\frac{T_{2}}{305}=(\frac{5}{1})^{\frac{1.4-1}{1.4}}`
T2 = 483.06 K
Combustion 2-3:
For the constant pressure heat addition process 2-3,
`q_{2-3}=Cp(T_{3}-T_{2})`
`300=1.005(T_{3}-483.06)`
T3 = 781.56 K
Reheating 4-5:
To obtain maximum work output, for the perfect reheating,
T5 = T3
`\mathbf{\therefore T_{5}=781.56 K}`
And the intermediate pressure (P4 or P5) is given by,
P4 = P5 = Pi
`P_{4}=P_{5}=\sqrt{P_{1}.P_{2}}`
`P_{4}=P_{5}= \sqrt{1 \times 5}`
`\mathbf{P_{4}=P_{5}}` = 2.23 bar
Isentropic expansion 3-4:
For the isentropic expansion 3-4, the relation between the pressure and temperature is given by,
`\frac{T_{3}}{T_{4}}=(\frac{P_{3}}{P_{4}})^{\frac{\gamma -1}{\gamma}}`
`\frac{781.56}{T_{4}}=(\frac{5}{2.23})^{\frac{1.4-1}{1.4}}`
T4 = 620.54 K
Isentropic expansion 5-6:
For the isentropic expansion in the low-pressure turbine, the relation between the pressure and temperature is given by,
`\frac{T_{5}}{T_{6}}=\frac{P_{5}}{P_{6}})^{\frac{\gamma -1}{\gamma}}`
`\frac{781.56}{T_{6}}=(\frac{2.23}{1})^{\frac{1.4-1}{1.4}}`
T6 = 621.5 K
Now the net work done by the gas turbine is given by,
`W_{\text{net}}=W_{\text{Turbine}}-W_{\text{Compressor}}`
`W_{\text{net}}=(W_{\text{HPT}}+W_{\text{LPT}})-W_{\text{Compressor}}`
`W_{\text{net}}=(W_{\text{3-4}}+W_{\text{5-6}})-W_{\text{1-2}}`
`W_{\text{Net}}=Cp(T_{3}-T_{4})+Cp(T_{5}-T_{6})-Cp(T_{2}-T_{1})`
`W_{\text{Net}}=1.005(781.56 – 620.54)+1.005(781.56-621.5)-1.005(483.06 – 305)`
WNet=143.73 KJ/Kg
FAQs:
-
How does a gas turbine reheater work?
The reheater is introduced between the two turbines working in series. thus the exhaust gases from the first turbine are heated into the reheater and then expanded into the second turbine to maximize the work output.
-
How does reheating affect gas turbine output?
The reheating helps to increase the net work output from the turbine.
Take a look at the other two methods which improves gas turbine efficiency: