The key difference for the shear modulus vs modulus of elasticity is that the shear modulus is the ratio of shear stress to the shear strain and the modulus of elasticity is the ratio of longitudinal stress and the longitudinal strain.
Contents:
Shear modulus:
The shear modulus or modulus of rigidity is the ratio of shear stress to the resulting shear strain in the object before the elastic limit and it is generally denoted by the symbol ‘G’. It can be also calculated by taking the slope of shear stress to the shear strain curve.
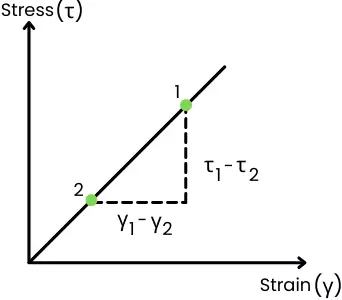
From the above stress-strain curve, the modulus of rigidity can be calculated as,
G = `\frac{\tau_{1} – \tau_{2}}{\gamma_{1} – \gamma_{2}}`
The shear modulus has an SI unit of Pascal or N/m² and it has a dimensional formula of [M¹L⁻¹T⁻²].
Modulus of elasticity:
The modulus of elasticity or the young’s modulus is defined as the ratio of longitudinal stress (`\sigma`) to the longitudinal strain (`\varepsilon`) before the elastic limit. and it is generally denoted by the symbol ‘E’.
Mathematically it can be expressed as,
Modulus of elasticity (E) = `\frac{\text{Longitudinal stress} (\sigma)}{\text{Longitudinal strain} (\varepsilon)}`
The modulus of elasticity has the same SI unit as stress which is N/m².
The modulus of elasticity can also be found by taking the slope of the stress-strain curve.
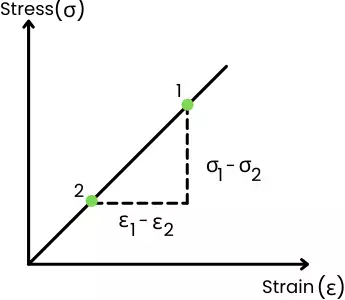
For the above stress-strain curve, the modulus of elasticity can be calculated as,
E = `\frac{\sigma_{1} – \sigma_{2}}{\varepsilon_{1} – \varepsilon_{2}}`
Shear modulus vs modulus of elasticity:
| Sr.No. | Shear modulus | Modulus of elasticity |
|---|---|---|
| 1 | Shear modulus is defined as the ratio of shear stress to the shear strain before the elastic limit. | Modulus of elasticity is defined as the ratio of longitudinal stress to the longitudinal strain before the elastic limit. |
| 2 | The shear modulus is the slope of the shear stress and shear strain curve. | The modulus of elasticity is the slope of the longitudinal stress and longitudinal strain curve. |
| 3 | Shear modulus is also known as the Modulus of rigidity. | Modulus of elasticity is also known as Young’s modulus named after the scientist Thomas Young. |
| 4 | The shear modulus is denoted by the symbol ‘G’. | The term modulus of elasticity is denoted by the letter ‘E’. |
| 5 | The formula of shear modulus is, G = `\frac{\text{Shear stress}}{\text{Shear strain}}` | The formula of modulus of elasticity is, E = `\frac{\text{Longitudinal stress}}{\text{Longitudinal strain}}` |
| 6 | The shear modulus is applicable where deformation occurs by sliding of one plane over another plane. | Modulus of elasticity is applicable where deformation occurs in the form of elongation or contraction. |
| 7 | It is applied in the case where the applied force is parallel to the resisting area. | It is applied in the case where the applied force is perpendicular to the resisting area. |
| 8 | For the same material, the shear modulus is mostly smaller than the modulus of elasticity. | The value of the modulus of elasticity for the same material is greater than the shear modulus. |
| 9 | It is used to analyze material subjected to torsional loading, shear loading. | It is used to analyze material subjected to compressive load, tensile load, or bending load. |
FAQs:
-
Is shear modulus the same as modulus of elasticity?
No, the shear modulus is the elastic constant for the shear loading, and the modulus of elasticity is the elastic constant for the longitudinal loading.
-
Is shear modulus greater than Young’s modulus?
No, for the same material the young’s modulus is greater than the shear modulus.
-
How do you calculate shear modulus from Young’s modulus and Poisson’s ratio?
By using young modulus and Poisson’s ratio, the shear modulus can be calculated with the use of the following relation,
E = 2G(1+μ)
Where,
E = Modulus of elasticity
G = Shear modulus
μ = Poisson’s ratio
I like it 👍👍👍👍