The torsion is the twisting of the object by the application of opposite torques at the ends of the object. The term torsional rigidity means the resistance offered by the object to avoid twisting. Continue reading to know torsional rigidity in detail.
In this article, we’re going to discuss:
- What is Torsional rigidity?
- Torsional rigidity equation:
- Torsional rigidity units:
3.1. Dimensional formula: - How to increase torsional rigidity?
- Torsional Rigidity Significance:
- How is torsional rigidity different from torsional stiffness?
- Solved Examples:
- FAQS:
What is Torsional rigidity?
Torsional rigidity is the product of shear modulus (G) and polar moment of inertia (J). It shows the resistance offered by a material to angular deformation.
In the below figure, the opposite torques (T) applied to the shaft are trying to twist the shaft and the torsional rigidity is working to oppose the twisting (angular deformation).
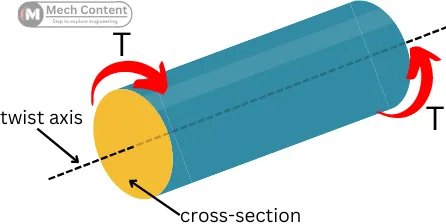
Torsional rigidity is also defined as the torque required to produce a unit radian angle of twist per unit length of the shaft.
The term torsional rigidity is expressed as,
Torsional rigidity = G x J
Thus, it depends on the shear modulus (G) and polar moment of inertia (J) of the object.
Let’s discuss, how these factors affect torsional rigidity.
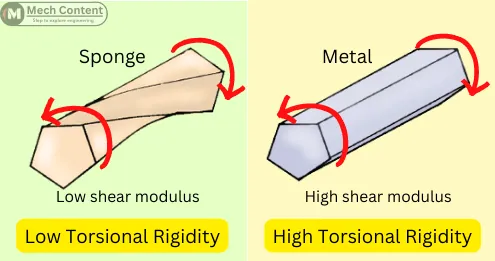
1] Higher Shear Modulus Means Greater Torsional Rigidity:
The below figure shows two objects of the same size made with a material having different shear moduli. When the same torque is applied to both objects, the object with less shear modulus shows more deformation than the other.
This happens because the object with less shear modulus has less torsional rigidity than another object.
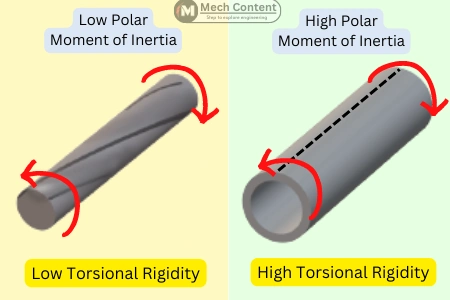
2] Higher Polar Moment Of Inertia Means Greater Torsional Rigidity:
The below figure shows two objects made with the same material but having different polar moment of inertia. When the same torque is applied to both objects, the object with a less polar moment of inertia shows more deformation than the other.
This happens because the object with a less polar moment of inertia has less torsional rigidity than another object.
Torsional rigidity equation:
The torsional rigidity of the component can be calculated by using the following formula:-
Torsional rigidity = G x J
From the torsional equation, the product G.J can also be written as,
`GJ =\frac{TL}{\theta }\cdots(\because\text{Torsional equation}\frac{T}{J} = \frac{G\theta }{L})`
Therefore, for the object subjected to the torque of T, the torsional rigidity can be given by,
`\mathbf{\text{Torsional rigidity} =\frac{TL}{\theta }}`
Where,
L = Length of a shaft (m)
θ = Angle of twist (Radian)
T = Torque (N.m)
Torsional rigidity units:
SI unit:
In the SI system, the unit of shear modulus (G) is N/m² or Pascal and the unit of polar moment of inertia is m⁴. Thus, the unit of torsional rigidity becomes,
GJ = `\frac{N}{m^{2}}`.m⁴ = N.m²
Hence, the SI unit of torsional rigidity is N.m².
FPS unit:
In the FPS system, the unit of shear modulus is lb/ft² and the unit of polar moment of inertia is ft⁴.
Thus, the unit of torsional rigidity becomes,
GJ = `\frac{lb}{ft^{2}}.ft^{4}` = lb.ft²
Hence, the FPS unit of torsional rigidity is lb.ft².
Dimensional formula:
The dimensional formula of shear modulus is [ML⁻¹T⁻²] and the dimensional formula of polar moment of inertia is [M⁰L⁴T⁰].
Therefore, the dimensional formula of modulus of rigidity is given by,
GJ = [ML⁻¹T⁻²][M⁰L⁴T⁰]
= [ML³T⁻²]
Therefore, the dimensional formula of the torsional rigidity is [ML³T⁻²].
How to increase torsional rigidity?
Here are some methods to increase.

1] Increase Polar moment of inertia (J):
Here are the two ways to increase the polar moment of inertia.
a) By changing the shape of the cross-section:
Choosing the cross-section with a high polar moment of inertia increases the torsional rigidity of the object.
e.g. a hollow circular cross-section of the same area has a higher value of the polar moment of inertia than a solid shaft.
b] Increasing size of cross-section:
Increasing the dimensions of the cross-section raises the polar moment of inertia (J). This leads to increased torsional rigidity.
2] increase the modulus of rigidity (G):
Modulus of rigidity is the material property. Hence, choose the material with a higher value of modulus of rigidity to increase the torsional rigidity.
Torsional Rigidity Significance:
1] Importance for shafts:
High torsional rigidity of the shaft means the shaft can work at a high torsional load with less twisting.
Shafts like camshafts must rotate without twisting to operate the engine valves accurately. Thus, for such shafts, torsional rigidity is a vital consideration.
2] Importance in automobile chassis:
The torsional rigidity is essential for the chassis to maintain its shape and alignment. Its high value indicates the chassis can bear high torsional stress with less deflection.
How is torsional rigidity different from torsional stiffness?
Torsional rigidity of the shaft is given by,
Torsional rigidity = G.J
Torsional stiffness is the torque required to twist an object by unit radian.
`\text{Torsional stiffness (K)} = \frac{T}{\theta} = \frac{GJ}{L}`
Replacing GJ with torsional rigidity,
`\text{Torsional stiffness (K)} = \frac{\text{torsional rigidity}}{L}`
Therefore, torsional stiffness can also be called torsional rigidity per unit length.
Solved Examples:
1] A circular shaft of radius 36 mm is made of aluminum with a shear modulus of 69 Gpa. Find the torsional rigidity of the shaft.
Given:
d = 36 mm
G = 69 GPa = 69 x 10³ N/mm²
Solution:-
The polar moment of inertia for the shaft is given by,
J = `\frac{\pi }{32}d^{4}` = `\frac{\pi }{32}36^{4}` = 164895.9 mm⁴
The torsional rigidity of the shaft is,
GJ = (69 x 10³) x (164895.9)
= 11.377 x 10⁹ N.mm²
Torsional rigidity = 11377 N.m²
2] Find torsional rigidity by using the following data,
T = 80 N.m
θ = 1°
L = 1 m
Given:
T = 80 N.m
θ = 1° = (1 x `\frac{\pi }{180}`) radian = 0.017 radian
L = 1 m
Solution:-
The torsional rigidity can be calculated as,
`\text{Torsional rigidity} =\frac{TL}{\theta } = \frac{800 \times 1}{0.017}`
= 47058.82 N.m²
Torsional rigidity = 47058.82 N.m²
FAQs:
-
What do you mean by torsional rigidity?
Torsional rigidity is the resistance offered by an object to angular deformation, which is equivalent to the product of shear modulus and polar moment of inertia.
-
What is the unit of torsional rigidity?
Its SI unit is N.m² and the FPS unit is lb.ft².
Read also: