Torsional stiffness: Definition, Formula, Units, of shaft

In this article, we’re going to discuss:

• What is torsional stiffness?
• Torsional stiffness formula:
• Why torsional stiffness is important?
• Torsional stiffness units:
• Torsional stiffness of shaft:
• Torsional stiffness vs Bending stiffness – Difference:
• How to calculate torsional stiffness?
• How to increase torsional stiffness?
• FAQs:

What is torsional stiffness?

Torsional stiffness is defined as the amount of torque required for twisting an object by unit radian. It is also known as the ratio of applied torque to the angle of twist (θ). It indicates how much the object is stiffer to withstand a torsional load.

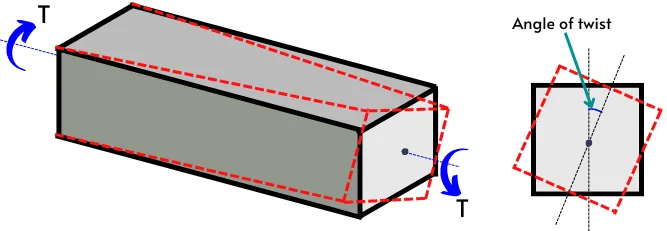
It is denoted by the symbol ‘K’ and can be evaluated as,

`\text{Torsional stiffness, K} =\frac{T}{\theta }`

Where,
T = torque
θ = Angle of twist in object

Higher torsional stiffness means that the object or a shaft is more capable to withstand torsional load and shows minimum torsional deformation.

Torsional stiffness mainly depends on the following factors:

• Modulus of rigidity or shear modulus of the material
• Polar moment of inertia of the cross-section

Torsional stiffness formula:

From the definition, the torsional stiffness equation is written as,

`K =\frac{T}{\theta }`

From the torsional equation, we can write,

`\frac{T}{\theta }= \frac{GJ}{L}`

Where,
G = Modulus of rigidity
J = Polar moment of inertia
L = Length of shaft

Therefore torsional stiffness equation can be written as,

`K =\frac{T}{\theta }= \frac{GJ}{L}`

As the product, ‘GJ’ indicates the torsional rigidity of an object, thus the torsional stiffness is also known as torsional rigidity per unit length of the object.

Why torsional stiffness is important?

Here are some cases, where torsional rigidity is an important consideration.

a] Stiffer shafts or axles:

The shafts and axles are directly subjected to the higher torsional loads.

For example, propeller shafts continuously deliver driving torque from the transmission. While wheel axles experience the driving torque as well as braking torque.

Thus shafts should be stiffer enough to continuously deliver power without causing failure.

b] Stiffness in chassis:

The chassis with better torsional stiffness offers a better ride, higher performance during handling, cornering, and efficient suspension. It is an important factor in chassis design.

The torsional stiffness of the chassis should not be lower as it will cause failure while cornering and it should not be very high as it causes difficulty in steering and less grip on the road.

c] Life of component:

Optimum torsional stiffness is essential to increase the life of the machine components subjected to the torsional cyclic loading.

Torsional stiffness units:

The SI and FPS units of the Torsional stiffness are as follows:-

i] SI unit:

In the SI system, the unit of torque is N.m and the unit of the angle of twist is radian, therefore the unit of the torsional stiffness is given by,

`K = \frac{T}{\theta }=\text{N.m/radian}`

∴ SI unit of torsional stiffness is N.m/radian.

ii] FPS unit:

In the FPS system, the unit of torque is lb.ft and the unit of the angle of twist is the radian. Hence the unit of the torsional stiffness in the FPS system is,

`K = \frac{T}{\theta }=\text{lb.ft/ radian}`

∴ FPS unit of torsional stiffness is lb.ft/radian.

Torsional stiffness of shaft:

1) Torsional stiffness of solid circular shaft:-

For a solid circular shaft of diameter ‘d’,

`J=\frac{\pi }{32}\times d^{4}`

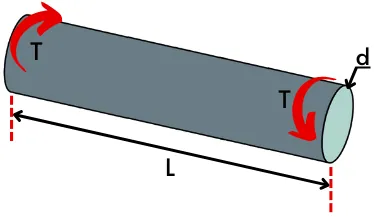
Therefore torsional stiffness of the solid circular shaft is,

`K =\frac{GJ}{L}=\frac{G}{L}\times [\frac{\pi }{32}\times d^{4}]`

`K =\frac{G\pi d^{4}}{32L}`

2) Torsional stiffness of hollow circular shaft:-

For a hollow circular shaft with an outside diameter of do and an inside diameter of di,

`J=\frac{\pi }{32}\times (do^{4}-di^{4})`

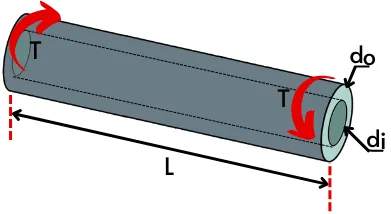
Hence torsional stiffness of the hollow shaft is,

`K =\frac{GJ}{L} = \frac{G}{L}\times [\frac{\pi }{32}\times (do^{4}-di^{4})]`

`K =\frac{G\pi (do^{4}-di^{4})}{32L}`

Torsional stiffness vs Bending stiffness – Difference:

Let’s see how torsional stiffness is differ from bending stiffness.

Sr. No.	Torsional stiffness	Bending stiffness
1	It indicates resistance to torsional deformation.	It indicates resistance to bending deformation.
2	It is given by, K = `\frac{T}{\theta}`	It is given by, BS = E.I
3	In the SI system, it is measured in N.m/radian.	It has a unit of N.m2.
4	It is important in the design of beams.	It is used in the design of an object subjected to a twisting load.

How to calculate torsional stiffness?

The torsional stiffness indicates torque per unit deflection in the shaft. It can be calculated experimentally or theoretically as follows,

1] Experimental method:-

In this method, the object is loaded under torsional load to find the angle of twist in a shaft. Then by using the below formula we can calculate the torsional stiffness of the object.

K = `\frac{\text{Torque}}{\text{angle of twist}}`

2] Theoretical method:-

In this method, it is necessary to know the shear modulus of the material and the geometry of the object.

1. Find the polar moment of inertia (J) of the cross-section area of the object that is perpendicular to the axis of twist.
2. Find the length of the object subjected to the twisting.
3. Find the shear modulus of the object.
4. Use the below formula,
   K = `\frac{GJ}{L}`

How to increase torsional stiffness?

Here are some ways to increase the torsional stiffness:

1] Choosing material with higher shear modulus:

Material with a higher shear modulus (modulus of rigidity) gives higher stiffness over torsional load.

2] Choosing the right geometry with a higher polar moment of inertia:

The geometry of the cross-section has a direct effect on the torsional stiffness of the object.

The geometry of the shape decides the polar moment of inertia which is the main factor for finding the torsional stiffness of the shaft.

3] Choosing hollow cross section instead of solid sections:

In the case of the hollow shaft, the mass of the shaft is spread outside, thus it provides a higher polar moment of inertia than the solid shaft of the same mass.

Thus it is better to choose hollow shafts over solid shafts to get the same torsional stiffness with reduced mass.

FAQs:

Read also:

• Torsional shear stress